
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,AD+EC=AB.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)△DEF可能是等腰直角三角形吗?为什么?
(4)请你猜想:当∠A为多少度时,∠EDF+∠EFD=120°,并请说明理由.

【答案】(1)证明见解析;(2)∠DEF=70°; (3)△DEF不可能是等腰直角三角形,理由见解析;(4)当∠A=60°时,∠EDF+∠EFD=120°,理由见解析.
【解析】
(1)首先根据条件证明△DBE≌△ECF,根据全等三角形的性质可得DE=FE,进而可得到△DEF是等腰三角形;
(2)由(1)中的全等得出∠BDE=∠CEF,再由角之间的转化,从而可求解∠DEF的大小;(3)由于AB=AC,可得∠B=∠C≠90°=∠DEF,从而可确定其不可能是等腰直角三角形;
(4)先猜想出∠A的度数,则可得∠EDF+∠EFD=120°,根据前面的推导过程知∠EDF+∠EFD=120°时,∠DEF=60°,再由∠B=∠DEF以及等腰三角形的性质继而推得猜想的正确性.
(1)∵AB=AC,
∴∠B=∠C,
∵AD+EC=AB,AB=AD+BD,
∴BD=CE,
在△BDE和△CEF中,
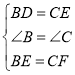 ,
,
∴△BDE≌△CEF(SAS)
∴DE=EF,
∴△DEF是等腰三角形;
(2)∵∠DEC=∠B+∠BDE,
即∠DEF+∠CEF=∠B+∠BDE,
由(1)知△BDE≌△CEF,
则∠BDE=∠CEF,
∴∠DEF=∠B,
∵∠A=40°,
∴∠B=∠C=![]() =70°,
=70°,
∴∠DEF=70°;
(3)△DEF不可能是等腰直角三角形,
∵AB=AC,
∴∠B=∠C≠90°,
由(2)知∠DEF=∠B,
∴∠DEF=∠B≠90°,
∴△DEF不可能是等腰直角三角形;
(4)当∠A=60°时,∠EDF+∠EFD=120°,
理由是:当∠EDF+∠EFD=120°时,
则∠DEF=180°-120°=60°,
∴∠B=∠DEF=60°,
∴∠A=180°-∠B-∠C=180°-60°-60°=60°,
∴当∠A=60°时,∠EDF+∠EFD=120°.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,我市某中学决定根据学生的兴趣爱好组建课外兴趣小组,因此学校随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
(1)学校这次调查共抽取了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“戏曲”所在扇形的圆心角度数为 ;
(4)设该校共有学生2000名,请你估计该校有多少名学生喜欢书法?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )

A. (3,4)或(2,4) B. (2,4)或(8,4)
C. (3,4)或(8,4) D. (3,4)或(2,4)或(8,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在生活中,人们经常通过一些标志性建筑确定位置,在数学中往往也是这样.
(1)将正整数如图1的方式进行排列:

小明同学通过仔细观察,发现每一行第一列的数字有一定的规律,所以每一行第一列的数字可以作为标志数,于是他认为第七行第一列的数字是 ,第7行、第5列的数字是 .
(2)方法应用
观察下面一列数:1,﹣2,3,﹣4,5,﹣6,7,…并将这列数按照如图2方式进行排列:
按照上述方式排列下去,
问题1:第10行从左边数第9个数是 ;
问题2:第n行有 个数;(用含n的代数式表示)
问题3:数字2019在第 行,从左边数第 个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织七年级学生体育健康抽测,(1)班25名学生的成绩(满分为100分)统计如下:
90,74,88,65,98,76,81,42,85,70,55,80,95,88,72,87,61,56,76,66,78,72,82,63,100.
(1)90分及以上为A级,75-89分为B级,60-74分为C级,60分以下为D级,请把下面表格补充完整,并将图中的条形图补充完整;
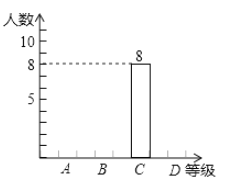
等级 | A | B | C | D |
人数 | 8 |
(2)该校七年级共有1000名学生,如果60分以上为合格,请估计七年级有多少人合格?
(3)请选择合适的统计图表示出抽测中每一个等级的人数占总人数的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC 中,AB=AC,中线 BD 将这个三角形的周长分成 15 和 18 两部分, 则这个三角形底边的长为( )
A. 9B. 13C. 9 或 13D. 10 或 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“阶梯水价”充分发挥市场、价格因素在水资源配置、水需求调节等方面的作用,拓展了水价上调的空间,增强了企业和居民的节水意识,避免了水资源的浪费.阶梯式计量水价将水价分为两段或者多段,每一分段都有一个保持不变的单位水价,但是单位水价会随着耗水量分段而增加.某地“阶梯水价”收费标准如下表(按月计算):
用水量 (单位:m3 ) | 单价(元/m3 ) |
不超出 | 2 |
超出 | 3 |
超出 | 5 |
例如:该地区某户居民3月份用水![]() m3,则应交水费为
m3,则应交水费为![]() (元
(元![]() .
.
根据上表的内容解答下列问题:
(1)用户甲5月份用水16 m3,则该用户5月份应交水费多少元?
(2)用户乙5月份交水费50元,则该用户5月份的用水量为多少m3?
(3) 用户丙5、6两个月共用水![]() m3,其中6月份用水量超过了
m3,其中6月份用水量超过了![]() m3,设5月份用水
m3,设5月份用水![]() m3,请用含
m3,请用含![]() 的式子表示该户居民5、6两个月共交的水费.
的式子表示该户居民5、6两个月共交的水费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB//CD,

(1) 求∠1+∠2+∠3的度数.
(2) ∠1+∠2+∠3+∠4 = .
根据以上的规律求∠1+∠2+∠3+…+∠n = .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com