
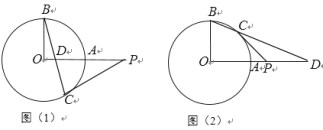
【题目】在⊙O中,半径OA丄OB,点D在OA或OA的延长线上(不与点O,A重合),直线BD交⊙O于点C,过C作⊙O的切线交直线OA于点P.
(1)如图(1),点D在线段OA上,若∠OBC=15°, 求∠OPC的大小;
(2)如图(2),点D在OA的延长线上,若∠OBC=65°,求∠OPC的大小.
【答案】(1)30°;(2)50°
【解析】
(1)连接OC,求出∠AOC=∠BOC - ∠BOA=60°,即可得到∠OPC=90° -∠AOC=30°;
(2)连接OC,求出∠AOC=∠AOB -∠BOC=40°,即可得到∠OPC=90° - ∠AOC = 50°.
解:(1)如图(1),连接OC.
∵PC是⊙O的切线,OC为⊙O的半径,
∴ OC⊥PC,
∴∠OCP=90°.
∵ OB=OC,
∴∠OCB=∠OBC=15°.
∴∠BOC=180° -∠OBC-∠OCB=150°.
∵ OB⊥OA,
∴∠BOA=90°.
∴∠AOC=∠BOC - ∠BOA=60°.
∴∠OPC=90° - ∠AOC=30°.
(2)如图(2),连接OC.
∵ CP是⊙O的切线,OC为⊙O的半径,
∴ OC⊥PC.
∴∠OCP = 90°.
∵ OB=OC,
∴∠OCB=∠OBC=65°.
∴∠BOC=180° -∠OBC -∠OCB=50°.
∵ OB⊥OA,
∴∠BOA=90°.
∴∠AOC=∠AOB -∠BOC=40°.
∴ ∠OPC=90° - ∠AOC = 50°.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
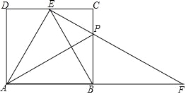
【题目】如图,在矩形ABCD中,AB=2,AD=![]() ,在边CD上有一点E,使EB平分∠AEC.若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.给出以下五个结论:
,在边CD上有一点E,使EB平分∠AEC.若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.给出以下五个结论:
①点B平分线段AF;②PF=![]() DE;③∠BEF=∠FEC;④S矩形ABCD=4S△BPF;⑤△AEB是正三角形.
DE;③∠BEF=∠FEC;④S矩形ABCD=4S△BPF;⑤△AEB是正三角形.
其中正确结论的序号是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD的对角线AC,BD交于点O,DE平分∠ADC交BC于点E,交AC与点F,且∠BCD=60°,BC=2CD,连接OE,则下列结论:①OE∥AB ②SABCD=BD·CD ③AO=2BO ④S△DOF=2S△EOF,其中成立的有( )
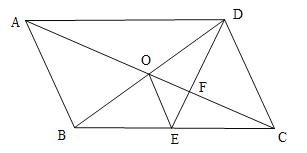
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
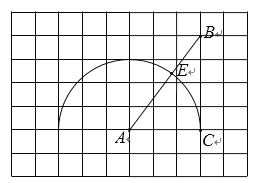
【题目】如图,在每个小正方形的边长为![]() 的网格中,点A,B,C在格点上,以点A为圆心、AC为半径的半圆交AB于点 E.
的网格中,点A,B,C在格点上,以点A为圆心、AC为半径的半圆交AB于点 E.
(1)BE的长为________;
(2)请用无刻度的直尺,在如图所示的网格中,找一点P(点P,C 在AB两侧),使PA=5,PE与半圆相切. 简要说明点P的位置是如何找到的.
查看答案和解析>>
科目:初中数学 来源: 题型:
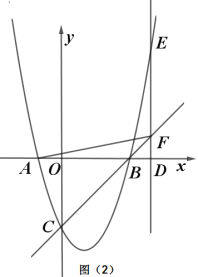
【题目】在平面直角坐标系中,抛物线![]() (
(![]() )与
)与![]() 轴交于A、B两点(点B在A的右侧),与
轴交于A、B两点(点B在A的右侧),与![]() 轴交于点C,D是抛物线的顶点.
轴交于点C,D是抛物线的顶点.
(1)当![]() 时,求顶点D 的坐标
时,求顶点D 的坐标
(2)若OD = OB,求![]() 的值;
的值;
(3)设E为A,B两点间抛物线上的一个动点(含端点A,B),过点E作EH⊥![]() 轴,垂足为H,交直线BC于点F. 记线段EF的长为t,若t的最大值为
轴,垂足为H,交直线BC于点F. 记线段EF的长为t,若t的最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为![]() ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
科目:初中数学 来源: 题型:
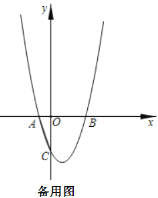
【题目】已知,在平面直角坐标系中,![]() 为坐标原点,抛物线
为坐标原点,抛物线![]()
![]() 分别交
分别交![]() 轴于
轴于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的侧),与
的侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图1,求![]() 的值;
的值;

(2)如图2,![]() 是
是![]() 轴上一点(不与点
轴上一点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的平行线,交抛物线于点
轴的平行线,交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
①当点![]() 在点
在点![]() 右侧时,连接AF,当
右侧时,连接AF,当![]() 时,求
时,求![]() 的长.
的长.
②当点![]() 在运动时,若
在运动时,若![]() 、
、![]() 、
、![]() 中有两条线段相等,此时点
中有两条线段相等,此时点![]() 的坐标_________.
的坐标_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
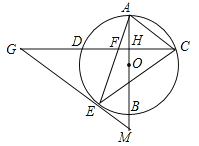
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=![]() ,AH=
,AH=![]() ,求EM的值.
,求EM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
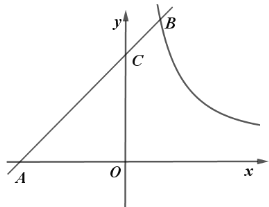
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,与
,与![]() 轴交于
轴交于![]() ,与
,与![]() 轴交于
轴交于![]() ,且
,且![]() .
.
(1)求一次函数与反比例函数的解析式;
(2)直接写出不等式:![]() 的解集;
的解集;
(3)![]() 是
是![]() 轴上一动点,直接写出
轴上一动点,直接写出![]() 叫的最大值和此时点
叫的最大值和此时点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com