
【题目】将9个数填入幻方的九个格中,使处于同一横行、同一竖列、同一斜对角线上的三个数的和相等,如图1所示。
(1)如图2所示,求![]() 的值;
的值;
(2)如图3所示:
①若![]() 求整式D;
求整式D;
②若![]() 求这九个整式的和是多少。
求这九个整式的和是多少。
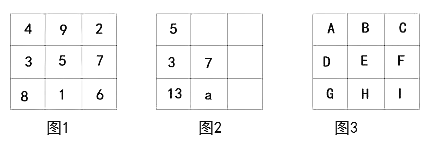
【答案】(1)-1;(2)①4a+4;②6a2+18a+9.
【解析】
(1)先根据第一列求出三个数的和,根据这个和求出右下角方格内的数,然后求出第三行中间的数a;
(2)①根据第一行求出三个数的和,和减去对角线的两个数C、E求出G,根据D=和-A-G即可解答;②再根据第一行的三个数的和求出左上角的数,然后求出第一列的第二个数,从而得解.
②根据同一横行、同一竖列、同一斜对角线上的三个数的和相等作出图形,根据题意列出关于a与x的方程,可得x=0,进一步求出这9个数的和即可.
解:(1)(5+3+13)-(5+7)=9,a=(5+3+13)-(13+9)=-1;
(2)①因为G=(A+B+C)-(C+E)=A+B-E=2a+7a+5-(5a+1)=4a+4,D=(A+B+C)-(A+G)=B+C-G=7a+5+6a-2-(4a+4)=9a-1;
②根据上面方法得表格:

根据第一列、第二列的和相等得;
(2a2+6)+( -a2-2a)+( a2+8a+x-3) =( 6a-3)+ (a2-2a-x+6)+( a2+2a)解得:x=0
所以这九个整式的和是:3[(2a2+6)+( -a2-2a)+( a2+8a-3)]=3(2a2+6a+3)= 6a2+18a+9.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(1)阅读下面的材料并把解答过程补充完整.
问题:在关于![]() ,
,![]() 的二元一次方程组
的二元一次方程组![]() 中,
中,![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
在关于![]() ,
,![]() 的二元一次方程组中,利用参数
的二元一次方程组中,利用参数![]() 的代数式表示
的代数式表示![]() ,
,![]() ,然后根据
,然后根据![]() ,
,![]() 列出关于参数
列出关于参数![]() 的不等式组即可求得
的不等式组即可求得![]() 的取值范围.解:由
的取值范围.解:由![]() ,解得
,解得 ,又因为
,又因为![]() ,
,![]() ,所以
,所以 解得____________.
解得____________.
(2)请你按照上述方法,完成下列问题:
①已知![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
②已知![]() ,在关于
,在关于![]() ,
,![]() 的二元一次方程组
的二元一次方程组![]() 中,
中,![]() ,
,![]() ,请直接写出
,请直接写出![]() 的取值范围(结果用含
的取值范围(结果用含![]() 的式子表示)____________.
的式子表示)____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
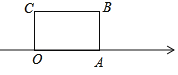
【题目】如图,面积为30的长方形OABC的边OA在数轴上,O为原点,OC=5.将长方形OABC沿数轴水平移动,O,A,B,C移动后的对应点分别记为O1, A1, B1, C1,移动后的长方形O1A1B1C1与原长方形OABC重叠部分的面积记为S
(1)当S恰好等于原长方形面积的一半时,数轴上点A1表示的数是多少?
(2)设点A的移动距离AA1=x
①当S=10时,求x的值;
②D为线段AA1的中点,点E在线段OO1上,且OE=![]() OO1,当点D,E所表示的数互为相反数时,求x的值.
OO1,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016甘肃省白银市)如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)x(﹣x)2(﹣x)3;(2)x3x5﹣(2x4)2+x10÷x2.
(3)(﹣0.125)2018×82019;(4)(a﹣b)10÷(b﹣a)3÷(b﹣a)3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数 y=kx+4(k≠0).
(1)当 x=-1 时,y=2,求此函数的表达式;
(2)函数图象与 x 轴、y 轴的交点分别为 A、B, 求出△AOB 的面积;
(3)利用图象求出当 y≤3 时,x 的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com