
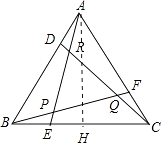
【题目】如图,△ABC是边长为m的正三角形,D,E,F分别在边AB,BC,CA上,AE,BF交于点P,BF,CD交于点Q,CD,AE交于点R,若 ![]() =
= ![]() =
= ![]() =k(0<k<
=k(0<k< ![]() ).
).
(1)求∠PQR的度数;
(2)求证:△ARD∽△ABE;
(3)求△PQR与△ABC的面积之比(用含k的代数式表示)
【答案】
(1)
解:∵ ![]() =
= ![]() =
= ![]() =k,△ABC是等边三角形,
=k,△ABC是等边三角形,
∴AB=CB=AC,∠ABC=∠BAC=∠ACB=60°,AD=BE=CF,
∴△ABE≌△BCF≌△CAD,
∴∠BAE=∠CBQ=∠ACD,∴∠ABP=∠BCQ=∠CAR,
∴△ABP≌△BCQ≌△CAR,
∴∠APB=∠BQC=∠ARC,
∴180°﹣∠APB=180°﹣BQC=180°﹣ARC,
即∠RPQ=∠PQR=∠PRQ,
∵∠RPQ+∠PQR+∠PRQ=180°,
∴∠RPQ=∠PQR=∠PRQ=60°.
∴∠PQR=60°.
(2)
解:∵△PQR是等边三角形,
∴∠PRQ=60°,
∴∠ARD=∠PRQ=60°,
∴∠ARD=∠ABC=∠ABE,
∵∠DAR=∠EAB,
∴△ARD∽△ABE
(3)
解:作AH⊥BC于H.易知BH=CH= ![]() ,AH=
,AH= ![]() m,BE=km,EH=
m,BE=km,EH= ![]() m﹣km,
m﹣km,
在Rt△AEH中,AE= ![]() =
= ![]() m,
m,
∵△ARD∽△ABE,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴AR= ![]() m,RD=
m,RD= ![]() m,PE=RD=
m,PE=RD= ![]() m,
m,
∴AP=AE﹣PE= ![]() m,
m,
当0<k< ![]() 时,RP=AP﹣AR=
时,RP=AP﹣AR= ![]() m,
m,
∵△PQR,△ABC都是等边三角形,
∴ ![]() =
= 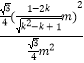 =
= ![]() .
.
【解析】(1)只要证明△ABP≌△BCQ≌△CAR,推出∠APB=∠BQC=∠ARC,推出180°﹣∠APB=180°﹣BQC=180°﹣ARC,即∠RPQ=∠PQR=∠PRQ,由此即可解决问题.(2)只要证明∠ARD=∠ABE=60°即可解决问题.(3)想办法求出等边三角形△PQR与△ABC的边长即可解决问题.
【考点精析】通过灵活运用等边三角形的性质和相似三角形的应用,掌握等边三角形的三个角都相等并且每个角都是60°;测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解即可以解答此题.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
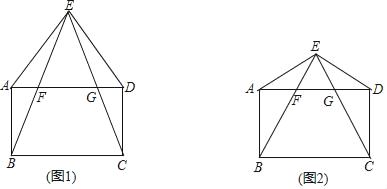
【题目】已知:点E为矩形ABCD外一点,连接AE,DE,且AE=DE,连接EB,EC分别与AD相交于点F,G.
(1)如图1,求证:∠ABE=∠DCE;
(2)如图2,若△BCE是等边三角形,且AE=AB,在不添加任何辅助线的情况下,请直接写出图2中四对全等的钝角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某项针对18﹣35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,m≥15时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,制作图表如下: 18﹣35岁青年人日均发微博条数统计表
m | 频数 | 百分数 |
A级(0≤m<5) | 90 | 0.3 |
B级(5≤m<10) | 120 | a |
C级(10≤m<15) | b | 0.2 |
D级(m≥15) | 30 | 0.1 |
请你根据以上信息解答下列问题:
(1)求a,b;
(2)补全频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8,点D、M分别在BC、AC上,Rt△BDE、Rt△EFG、Rt△GHI、Rt△IJK、Rt△KMA的斜边都在AB上,则五个小直角三角形的周长和为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践探究
在数学实践课上,小明提出了这样的问题:分数![]() 可以写为小数形式,即0.
可以写为小数形式,即0.![]() 反过来,无限循环小数0.
反过来,无限循环小数0. ![]() 写成分数形式即为
写成分数形式即为![]() .那么无限循环小数0.
.那么无限循环小数0. ![]() 应怎样化为分数呢?
应怎样化为分数呢?
小明是这样思考的:
在学习解一元一次方程时,当变形到ax=b(a≠0)形式后,通过系数化1,两边同时除以a,得到方程的解x=![]() ,
,![]() 就是分数形式.
就是分数形式.
设0. ![]() =x,即x=0.777…,又10x=7.77…,这里x、0.777…、10x、7.77…存在着关系,根据这一关系我就可以找到相等关系,列出方程.
=x,即x=0.777…,又10x=7.77…,这里x、0.777…、10x、7.77…存在着关系,根据这一关系我就可以找到相等关系,列出方程.
请你阅读小明的思考过程,把无限循环小数0. ![]() 化为分数的过程写出来.
化为分数的过程写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图(图2),支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得DE=20厘米,DC=40厘米,∠AED=58°,∠ADE=76°. 
(1)求椅子的高度(即椅子的座板DF与地面MN之间的距离)(精确到1厘米)
(2)求椅子两脚B、C之间的距离(精确到1厘米)(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,sin76°≈0.97.cos76°≈0.24,tan76°≈4.00)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y= ![]() 的图象与性质. 下面是小文的探究过程,请补充完整:
的图象与性质. 下面是小文的探究过程,请补充完整:
(1)函数y= ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)如表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 2 | 3 | 4 | 5 | … |
y | … | ﹣ | ﹣ | ﹣ | 0 | 2 | | | | … |
如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.
①观察图中各点的位置发现:点A1和B1 , A2和B2 , A3和B3 , A4和B4均关于某点中心对称,则该点的坐标为;
②小文分析函数y= ![]() 的表达式发现:当x<1时,该函数的最大值为0,则该函数图象在直线x=1左侧的最高点的坐标为;
的表达式发现:当x<1时,该函数的最大值为0,则该函数图象在直线x=1左侧的最高点的坐标为;
(3)小文补充了该函数图象上两个点( ![]() ,﹣
,﹣ ![]() ),(
),( ![]() ,
, ![]() ), ①在上图中描出这两个点,并画出该函数的图象;
), ①在上图中描出这两个点,并画出该函数的图象;
②写出该函数的一条性质: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com