
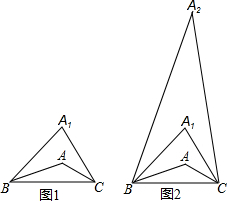
 在△ABC中,∠A=160°.
在△ABC中,∠A=160°.分析 由∠A的度数结合三角形内角和定理可得出∠ABC+∠ACB=20°,由∠A1BA=∠ABC、∠A1CA=∠ACB结合三角形内角和定理可求出∠A1=140°,同理可求出∠A2=120°、∠A3=100°、…、∠An=180°-20(n+1)°,令∠An=0°求出n值,由三角形的内角不为0度即可得出至多能进行7步.
解答 解:∵∠A=160°,
∴∠ABC+∠ACB=180°-∠A=20°.
∵∠A1BA=∠ABC,∠A1CA=∠ACB,
∴∠A1BC+∠A1CB=2(∠ABC+∠ACB)=40°,
∴∠A1=180°-(∠A1BC+∠A1CB)=140°.
同理,可得:∠A2=120°,∠A3=100°,…,∠An=180°-20(n+1)°,
∴当n=8时,∠A8=0°,
∴至多能进行7步.
故答案为:140°;7.
点评 本题考查了三角形内角和定理,根据三角形内角和定理找出∠An=180°-20(n+1)°是解题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
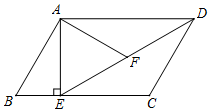 如图,平行四边形ABCD中,过点A作AE⊥BC于E,连接DE,F为DE中点,且∠BAE=∠DEC,∠B=60°.
如图,平行四边形ABCD中,过点A作AE⊥BC于E,连接DE,F为DE中点,且∠BAE=∠DEC,∠B=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
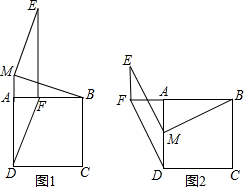 正方形ABCD的边长是5,点M是直线AD上一点,连接BM,将线段BM绕点M逆时针旋转90°得到线段ME,在直线AB上取点F,使AF=AM,且点F与点E在AD同侧,连接EF,DF.
正方形ABCD的边长是5,点M是直线AD上一点,连接BM,将线段BM绕点M逆时针旋转90°得到线段ME,在直线AB上取点F,使AF=AM,且点F与点E在AD同侧,连接EF,DF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
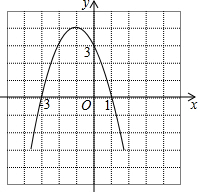 如图所示的是二次函数y=ax2+bx+c的图象,有下列结论:
如图所示的是二次函数y=ax2+bx+c的图象,有下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com