
如图,等腰梯形ABCD放置在平面直角坐标系中,已知A(-2,0)、B(6,0)、A(0,3),反比例函数的图象经过点C.
(1)求C点坐标和反比例函数的解析式;(6分)
(2)将等腰梯形ABCD向上平移 个单位后,使点B恰好落在双曲线上,求
个单位后,使点B恰好落在双曲线上,求 的值.(4分)
的值.(4分)
(1)(4,3), ;(2)2.
;(2)2.
解析试题分析:(1)C点的纵坐标与D的纵坐标相同,过点C作CE⊥AB于点E,则△AOD≌△BEC,即可求得BE的长度,则OE的长度即可求得,即可求得C的横坐标,然后利用待定系数法即可求得反比例函数的解析式;(2)得出B′的坐标是(6,m),代入反比例函数的解析式,即可求出答案.
试题解析:(1)如图,过点C作CE⊥AB于点E,
∵四边形ABCD是等腰梯形,∴AD=BC,DO=CE.
∴△AOD≌△BEC(HL. ∴AO=BE=2.
∵BO=6,∴DC=OE=4,∴C(4,3).
设反比例函数的解析式为 (k≠0),
(k≠0),
∵反比例函数的图象经过点C,∴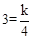 ,解得k=12.
,解得k=12.
∴反比例函数的解析式为 .
.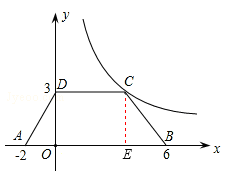
(2)将等腰梯形ABCD向上平移m个单位后得到梯形A′B′C′D′,
∴点B′(6,m),
∵点B′(6,m)恰好落在双曲线 上,∴当x=6时,
上,∴当x=6时, . 即m=2.
. 即m=2.
考点:1.反比例函数综合题;2.等腰梯形的性质;3.全等三角形的判定和性质;4.待定系数法;5.曲线上点的坐标与方程的关系;6.平移的性质.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:解答题
如图,将透明三角形纸片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数 图象的两支上,且PB⊥x于点C,PA⊥y于点D,AB分别与x轴,y轴相交于点E、F.已知B(1,3).
图象的两支上,且PB⊥x于点C,PA⊥y于点D,AB分别与x轴,y轴相交于点E、F.已知B(1,3).
(1)k= ;
(2)试说明AE=BF;
(3)当四边形ABCD的面积为 时,求点P的坐标.
时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一次函数 的图像与反比例函数
的图像与反比例函数 的图象交于A(-2,1),B(1,n)两点.
的图象交于A(-2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△OAB的面积.
(3)写出反比例函数值大于一次函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
定义:如图,若双曲线 与它的其中一条对称轴
与它的其中一条对称轴 相交于两点A,B,则线段AB的长称为双曲线
相交于两点A,B,则线段AB的长称为双曲线 的对径.
的对径.
(1)求双曲线 的对径;
的对径;
(2)若某双曲线 对径是
对径是 .求k的值;
.求k的值;
(3)仿照上述定义,请你定义双曲线 的对径.
的对径.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,反比例函数y=(x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).
(1)直接写出B、C、D三点的坐标;
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,一次函数 与反比例函数
与反比例函数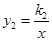 的图象交于点
的图象交于点 和
和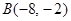 ,与
,与 轴交于点
轴交于点 .(1)
.(1) ,
, ;
;
(2)根据函数图象可知,当 时,
时, 的取值范围是 ;
的取值范围是 ;
(3)过点 作
作 轴于点
轴于点 ,点
,点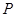 是反比例函数在第一象限的图象上一点,设直线
是反比例函数在第一象限的图象上一点,设直线 与线段
与线段 交于点
交于点 ,当
,当 时,求点
时,求点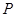 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,一次函数 (k≠0)的图象与反比例函数
(k≠0)的图象与反比例函数 (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且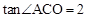 .
.
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)在x轴上求点E,使△ACE为直角三角形.(直接写出点E的坐标)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,反比例函数 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点.
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.
(3)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com