
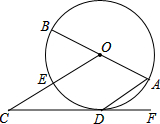
 如图,AB是⊙O的直径,点D是⊙O上的一点,OC∥AD交⊙O于点E,点F在CD的延长线上,∠BOC+∠ADF=90°.
如图,AB是⊙O的直径,点D是⊙O上的一点,OC∥AD交⊙O于点E,点F在CD的延长线上,∠BOC+∠ADF=90°.分析 (1)连结OD,由OC∥AD得到∠BOC=∠A,而∠ODA=∠A,则∠ODA=∠BOC,由于∠BOC+∠ADF=90°,所以∠ODA+∠ADF=90°,然后根据切线的判定定理得到结论;
(2)延长CO交⊙O于H,于是得到EH=AB=6,根据切割线定理即可得到结论.
解答  (1)证明:连结OD,如图,
(1)证明:连结OD,如图,
∵OC∥AD,
∴∠BOC=∠A,
而OD=OA,
∴∠ODA=∠A,
∴∠ODA=∠BOC,
∵∠BOC+∠ADF=90°,
∴∠ODA+∠ADF=90°,
即∠ODF=90°,
∴OD⊥DF,
∴CD是⊙O的切线;
(2)延长CO交⊙O于H,
∴EH=AB=6,
∵CD是⊙O的切线,
∴CD2=CE•CH,
即42=CE(CE+6),
∴CE=2(负值舍去).
点评 本题考查了切线的判定定理,切割线定理,知道经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点E是正方形ABCD的边BC上的一点,把线段AE绕点E顺时针旋转90°得到线段EF,连接CF,AF.
如图,已知点E是正方形ABCD的边BC上的一点,把线段AE绕点E顺时针旋转90°得到线段EF,连接CF,AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com