
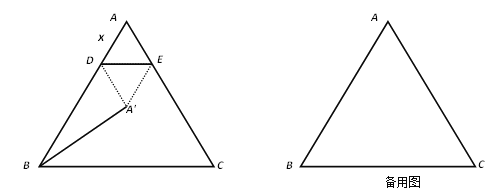
【题目】如图,在△ABC中,AB=AC=5,BC=6,点D为AB边上的一动点(D不与A、B重合),过D作DE∥BC,交AC于点E.把△ADE沿直线DE折叠,点A落在点A'处.连结BA',设AD=x,△ADE的边DE上的高为y.
(1) 求出y与x的函数关系式;
(2) 若以点A'、B、D为顶点的三角形与△ABC 相似,求x的值;
(3) 当x取何值时,△A' DB是直角三角形.
【答案】(1)y=![]() (0<x<5).(2)x=
(0<x<5).(2)x=![]() .(3)当x=
.(3)当x=![]() 、x=
、x=![]() 时,△A'DB是直角三角形.
时,△A'DB是直角三角形.
【解析】试题分析:(1)先过A点作AM⊥BC,得出BM=![]() BC=3,再根据DE∥BC,得出AN⊥DE,即y=AN,再在Rt△ABM中,求出AM的值,再根据DE∥BC,求出△ADE∽△ABC,即可求出y与x的函数关系式;
BC=3,再根据DE∥BC,得出AN⊥DE,即y=AN,再在Rt△ABM中,求出AM的值,再根据DE∥BC,求出△ADE∽△ABC,即可求出y与x的函数关系式;
(2)根据△A'DE由△ADE折叠得到,得出AD=A'D,AE=A'E,再由(1)可得△ADE是等腰三角形,得出AD=A'D,AE=A'E,即可证出四边形ADA'E是菱形,得出∠BDA'=∠BAC,再根据∠BAC≠∠ABC,∠BAC≠∠C,得出∠BDA'≠∠ABC,∠BDA'≠∠C,从而证出△BDA'∽△BAC,即可求出x的值;
(3)先分三种情况进行讨论;第一种情况当∠BDA′=90°,得出∠BDA'≠90°;第二种情况当∠BA'D=90°,根据∠BAM<90°,∠BA'D<∠BAM,可得∠BA'D≠90°;第三种情况当∠A'BD=90°,根据∠A'BD=90°,∠AMB=90°,得出△BA'M∽△ABM,即可求出BA′的值,再在Rt△DBA'中,根据DB2+A'B2=A'D2,求出x的值,即可证出△A′DB是直角三角形;
试题解析:(1)如图1,过A点作AM⊥BC,垂足为M,交DE于N点,则BM=![]() BC=3,
BC=3,
∵DE∥BC,
∴AN⊥DE,即y=AN.
在Rt△ABM中,AM=![]() =4,
=4,
∵DE∥BC,
∴△ADE∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴y=![]() (0<x<5).
(0<x<5).
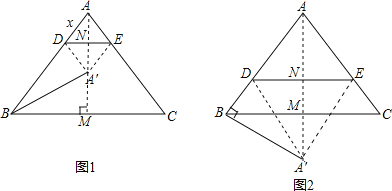
(2)∵△A'DE由△ADE折叠得到,
∴AD=A'D,AE=A'E,
∵由(1)可得△ADE是等腰三角形,
∴AD=AE,
∴A'D=A'E,
∴四边形ADA'E是菱形,
∴AC∥DA',
∴∠BDA'=∠BAC,
又∵∠BAC≠∠ABC,
∴∠BDA'≠∠ABC,
∵∠BAC≠∠C,
∴∠BDA'≠∠C,
∴有且只有当BD=A'D时,△BDA'∽△BAC,
∴当BD=A'D,即5-x=x时,x=![]() .
.
(3)第一种情况:∠BDA'=90°,
∵∠BDA'=∠BAC,而∠BAC≠90°,
∴∠BDA'≠90°.
第二种情况:∠BA'D=90°,
∵在Rt△BA'D中,DB2-A'D2=A'B2,
在Rt△BA'M中,A'M2+BM2=A'B2,
∴DB2-A'D2=A'M2+BM2,
∴(5-x)2-x2=(4-![]() x)2+(3)2,
x)2+(3)2,
解得x=![]() ;
;
第三种情况:∠A'BD=90°,
∵∠A'BD=90°,∠AMB=90°,
∴△BA'M∽△ABM,
即![]() ,
,
∴BA'=![]() ,
,
在Rt△DBA'中,DB2+A'B2=A'D2,
(5-x)2+![]() =x2,
=x2,
解得:x=![]() .
.
综上可知当x=![]() 或
或![]() 时,△A'DB是直角三角形.
时,△A'DB是直角三角形.


科目:初中数学 来源: 题型:
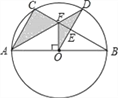
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2![]() .
.
(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列叙述中,正确的是( )
A. 在同一平面内,两条直线的位置关系有三种,分别是相交、平行、垂直
B. 不相交的两条直线叫平行线
C. 两条直线的铁轨是平行的
D. 我们知道,对顶角是相等的,那么反过来,相等的角就是对顶角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用公式法解﹣x2+3x=1时,先求出a、b、c的值,则a、b、c依次为( )
A.﹣1,3,1B.1,3,1C.﹣1,3,﹣1D.1,﹣3,﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于正数 ![]() ,用符号
,用符号 ![]() 表示
表示 ![]() 的整数部分,例如:
的整数部分,例如: ![]() ,
, ![]() ,
, ![]() .点
.点 ![]() 在第一象限内,以A为对角线的交点画一个矩形,使它的边分别与两坐标轴垂直. 其中垂直于
在第一象限内,以A为对角线的交点画一个矩形,使它的边分别与两坐标轴垂直. 其中垂直于 ![]() 轴的边长为
轴的边长为 ![]() ,垂直于
,垂直于 ![]() 轴的边长为
轴的边长为 ![]() ,那么,把这个矩形覆盖的区域叫做点A的矩形域.例如:点
,那么,把这个矩形覆盖的区域叫做点A的矩形域.例如:点 ![]() 的矩形域是一个以
的矩形域是一个以 ![]() 为对角线交点,长为3,宽为2的矩形所覆盖的区域,如图1所示,它的面积是6.
为对角线交点,长为3,宽为2的矩形所覆盖的区域,如图1所示,它的面积是6.

图1 图2
根据上面的定义,回答下列问题:
(1)在图2所示的坐标系中画出点 的矩形域,该矩形域的面积是;
(2)点 ![]() 的矩形域重叠部分面积为1,求
的矩形域重叠部分面积为1,求 ![]() 的值;
的值;
(3)已知点 ![]() 在直线
在直线 ![]() 上, 且点B的矩形域的面积
上, 且点B的矩形域的面积 ![]() 满足
满足 ![]() ,那么
,那么 ![]() 的取值范围是 . (直接写出结果)
的取值范围是 . (直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2+6x﹣3=0,原方程可变形为( )
A.(x+3)2=9B.(x+3)2=12C.(x+3)2=15D.(x+3)2=39
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
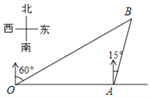
A. 3![]() km B. 3
km B. 3![]() km C. 4km D. (3
km C. 4km D. (3![]() -3)km
-3)km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一道题“计算:(2m4-4m3n-2m2n2)-(m4-2m2n2)+(-m4+4m3n-n3)的值,其中![]() ,n=-1.”小强不小心把
,n=-1.”小强不小心把![]() 错抄成了
错抄成了![]() ,但他的计算结果却也是正确的,你能说出这是为什么吗?
,但他的计算结果却也是正确的,你能说出这是为什么吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com