
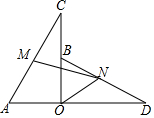
 如图,OA=OB,OC=OD,∠AOB=∠COD=90°,M,N分别为AC,BD的中点,连接MN,ON,求证:∠MNO=45°.
如图,OA=OB,OC=OD,∠AOB=∠COD=90°,M,N分别为AC,BD的中点,连接MN,ON,求证:∠MNO=45°. 分析 连接OM,根据全等三角形的性质得到AC=BD,∠C=∠D,根据直角三角形的性质得到OM=$\frac{1}{2}$AC,ON=$\frac{1}{2}$BD,根据等腰三角形的性质得到∠MOC=∠C=∠D=∠MOD,推出△MPN是等腰直角三角形,于是得到结论.
解答  证明:连接OM,
证明:连接OM,
在△AOC与△BOD中,$\left\{\begin{array}{l}{AO=BO}\\{∠AOB=∠COD}\\{OC=OD}\end{array}\right.$,
∴△AOC≌△BOD,
∴AC=BD,∠C=∠D,
∵M,N分别为AC,BD的中点,
∴OM=$\frac{1}{2}$AC,ON=$\frac{1}{2}$BD,
∴OM=ON,
∴OM=CM=ON=DN,
∴∠MOC=∠C=∠D=∠MOD,
∴∠COM+∠BON=90°,
∴△MPN是等腰直角三角形,
∴∠MNO=45°.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的判定和性质,直角三角形的性质,证得△MON是等腰直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>$\frac{2}{3}$ | B. | m≤$\frac{2}{3}$ | C. | m>-$\frac{2}{3}$ | D. | m≤-$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明骑自行车从甲地出发,途径乙地休息半小时后,继续骑行至目的地丙地,小明出发1小时后,恰有一辆货车从甲地出发,沿小明行进路线前往丙地,在丙地完成2小时装卸工作后按原路返回甲地,小明与货车行驶速度均保持不变,并且货车行驶速度是小明行驶速度的2.5倍,如图是小明、货车离甲地的路程y(km)与小明离开甲地时间x(h)的函数关系图象,请回答下列问题:
小明骑自行车从甲地出发,途径乙地休息半小时后,继续骑行至目的地丙地,小明出发1小时后,恰有一辆货车从甲地出发,沿小明行进路线前往丙地,在丙地完成2小时装卸工作后按原路返回甲地,小明与货车行驶速度均保持不变,并且货车行驶速度是小明行驶速度的2.5倍,如图是小明、货车离甲地的路程y(km)与小明离开甲地时间x(h)的函数关系图象,请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ﹒2个 | B. | ﹒3个 | C. | ﹒4个 | D. | ﹒5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,A(-1,5),B(-2,1),C(-4,3)
在平面直角坐标系中,A(-1,5),B(-2,1),C(-4,3)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com