
分析 首先应用乘法分配律,可得($\sqrt{\frac{1}{3}}$+$\sqrt{27}$)×$\sqrt{3}$=$\sqrt{\frac{1}{3}}$×$\sqrt{3}$+$\sqrt{27}$×$\sqrt{3}$;然后根据二次根式的混合运算顺序,先计算乘法,再计算加法,求出算式($\sqrt{\frac{1}{3}}$+$\sqrt{27}$)×$\sqrt{3}$的值是多少即可.
解答 解:($\sqrt{\frac{1}{3}}$+$\sqrt{27}$)×$\sqrt{3}$
=$\sqrt{\frac{1}{3}}$×$\sqrt{3}$+$\sqrt{27}$×$\sqrt{3}$
=1+9
=10
点评 此题主要考查了二次根式的混合运算,要熟练掌握,解答此题的关键是要明确:①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.②在运算中每个根式可以看做是一个“单项式”,多个不同类的二次根式的和可以看作“多项式”.


科目:初中数学 来源: 题型:解答题
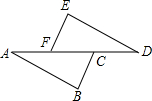 如图,已知BC∥EF,BC=EF,AF=DC,那么AB=DE吗?请说明你的理由.小明的解题过程如下,请你将每一步的理由补充完整.
如图,已知BC∥EF,BC=EF,AF=DC,那么AB=DE吗?请说明你的理由.小明的解题过程如下,请你将每一步的理由补充完整.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点B,C是线段AD的三等分点,以BC为直径作⊙O,点P是圆上异于B,C的任意一点,连接PA,PB,PC,PD.
如图,点B,C是线段AD的三等分点,以BC为直径作⊙O,点P是圆上异于B,C的任意一点,连接PA,PB,PC,PD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com