
如图所示,已知二次函数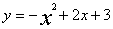 与坐标轴分别交于A、D、B三点,顶点为C。【原创】
与坐标轴分别交于A、D、B三点,顶点为C。【原创】
(1)求tan∠BAC
(2)在y轴上是否存在一点P,使得△DOP与△ABC相似,如果存在,求出点P的坐标,如果不存在,说明理由。
(3)Q是抛物线上一动点,使得以A、B、C、Q为端点的四边形是一个梯形,请直接写出满足条件的Q点的坐标。(不要求写出解题过程)
 |
解:(1)把y=0代入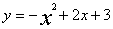 ,得
,得 。
。
解得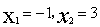
 即A(3,0),D(-1,0)
即A(3,0),D(-1,0)
把x=0代入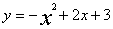 ,得y=3
,得y=3
∴B(0,3)
把x=1代入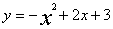
y=4,即C(1,4)。
过点C作CE⊥y轴,垂足为E。
∵△AOB和△BCE都是等腰直角三角形
∴∠ABC=90°且BC=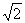 ,AB=
,AB= 。
。
∴tan∠BAC= 。。。。。4分
。。。。。4分
(2)①P在原点时,
∵PD=1,BP=3,∠BPD=∠ABC,且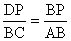
即△DOP∽△ABC。。。。。。。。。。。。。。。。2分
②当P在y轴负半轴时,设P(0,a)
由①知∠DBP=∠BAC。
∴只需∠BDP=Rt∠即可。
此时,易证△BDO∽△DOP
∴
∴OP=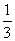
∴P(0,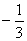 )。。。。。。。。。。。。。。。。2分
)。。。。。。。。。。。。。。。。2分
②当P在y轴正半轴时,显然△BDP不可能为Rt△。
∴所以满足题意的P点为(0,0)或(0,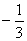 )。
)。
(3)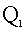 (-2,-5),
(-2,-5),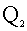 (4,-5),
(4,-5), (2,3)
(2,3)


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
(1)如图1,在等边△ABC中,点M是边BC上的任意一点(不含端点B、C),联结AM,以AM为边作等边△AMN,联结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是边BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是边BC上的任意一点(不含端点B、C),联结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.联结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
 xkb1.com
xkb1.com
查看答案和解析>>
科目:初中数学 来源: 题型:
已知△ABC,用直尺和圆规,根据下列要求作图(保留作图痕迹,不写作法)
(1)作∠ABC的平分线BD交AC于点D;
 (2)作线段BD的垂直平分线交AB于点E,交BC于点F。由(1)(2)可得,你发现了BEDF是什么四边形?(原创)
(2)作线段BD的垂直平分线交AB于点E,交BC于点F。由(1)(2)可得,你发现了BEDF是什么四边形?(原创)
查看答案和解析>>
科目:初中数学 来源: 题型:
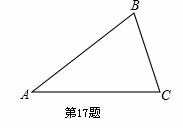
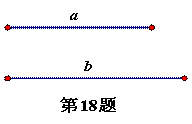
古希腊数学家丢番图(公元250年前后)在《算术》中就提到了一元二次方程的问题,不过当时古希腊人还没有寻求到它的求根公式,只能用图解等方法来求解。在欧几里得的《几何原本》中,形如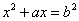 (a>0,b>0)的方程的图解法是:以
(a>0,b>0)的方程的图解法是:以 和b为两直角边做Rt△ABC,再在斜边上截取BD=
和b为两直角边做Rt△ABC,再在斜边上截取BD= ,则AD的长就是所求方程的解。
,则AD的长就是所求方程的解。
(1)请利用所给的线段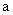 和线段b,作出方程的解。
和线段b,作出方程的解。
(2)说说上述求法的不足之处
查看答案和解析>>
科目:初中数学 来源: 题型:
在△ABC中,∠C=90°,AC=12,BC=5,现在AC为轴旋转一周得到一个圆锥。则该圆锥的侧面积为 ( )
(A)130π (B)90π (C)25π (D)65π
查看答案和解析>>
科目:初中数学 来源: 题型:
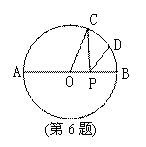
如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,弧AC的度数为100°弧BC=2弧BD,动点P在线段AB上,则PC+PD的最小值为 ( )(原创)
A.R B.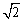 R C.
R C.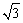 R D.
R D. R
R
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com