
【题目】如图,已知A,B两点的坐标分别为(2 ![]() ,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为 .
,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为 . 
【答案】(4 ![]() ,4)
,4)
【解析】解:∵A,B两点的坐标分别为(2 ![]() ,0),(0,10),
,0),(0,10),
∴OB=10,OA=2 ![]() ,
,
∴AB= ![]() =4
=4 ![]() ,
,
∵∠AOB=90°,
∴AB是直径,CM=2 ![]() ,
,
∴Rt△AOB外接圆的圆心为AB中点,
∴C点坐标为( ![]() ,5),
,5),
过点C作CF∥OA,过点M作ME⊥OA于E交CF于F,作CN⊥OE于N,如图所示:
则ON=AN= ![]() OA=
OA= ![]() ,
,
设ME=x,
∵∠AOM=30°,
∴OE= ![]() x
x
∴∠CFM=90°,
∴MF=5﹣x,CF= ![]() x﹣
x﹣ ![]() ,CM=2
,CM=2 ![]() ,
,
在△CMF中,根据勾股定理得:( ![]() x﹣
x﹣ ![]() )2+(5﹣x)2=(2
)2+(5﹣x)2=(2 ![]() )2 ,
)2 ,
解得:x=4或x=0(舍去),
∴OE= ![]() x=4
x=4 ![]()
故答案为:(4 ![]() ,4).
,4).
由勾股定理求出AB的长,由圆周角定理得出AB为直径,求出半径和圆心C的坐标,过点C作CF∥OA,过点P作ME⊥OA于E交CF于F,作CN⊥OE于N,设ME=x,得出OE= ![]() x,在△CMF中,根据勾股定理得出方程,解方程即可.
x,在△CMF中,根据勾股定理得出方程,解方程即可.


科目:初中数学 来源: 题型:
【题目】数学课上,老师出示了如下的题目:如图(1),在等边△ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,试判断AE和BD的大小关系,并说明理由.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图(2),确定线段AE与DB的大小关系,请你直接写出结论:AE DB(填“>”,“<”或“=”);
(2)特例启发,解答题目
如图(1),试判断AE和BD的大小关系,并说明理由;
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC;若△ABC的边长为1,AE=2,请画出图形,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上, 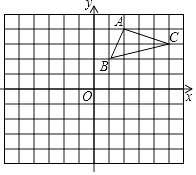
(1)①画出△ABC关于x轴对称的△A1B1C1 .
②画出△ABC绕原点O旋转180°后的△A2B2C2 , 并写出A2、B2、C2的坐标
(2)假设每个正方形网格的边长为1,求△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+ax+a﹣2=0
(1)若该方程的一个根为1,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com