Question

9．如图，在Rt△ABC中，∠BAC=90°，∠B=60°，以边上AC上一点O为圆心，OA为半径作⊙O，⊙O恰好经过边BC的中点D，并与边AC相交于另一点F．
（1）求证：BD是⊙O的切线；
（2）若BC=2$\sqrt{3}$，E是半圆$\widehat{AGF}$上一动点，连接AE、AD、DE．
填空：
①当$\widehat{AE}$的长度是$\frac{2}{3}$π时，四边形ABDE是菱形；
②当$\widehat{AE}$的长度是$\frac{1}{3}$π或π时，△ADE是直角三角形．

Answer 1

分析 （1）连接OD，如图，利用斜边上的中线性质得DB=DA=DC，则可判断△ABD为等边三角形得到∠DAB=∠ADB=60°，∠DAC=∠C=30°，然后计算出∠ODB=90°，从而根据切线的判定定理可判定BD是⊙O的切线；
（2）解：①利用△ABD为等边三角形得到AB=BD=AD=CD=$\sqrt{3}$，则可计算出OD=$\frac{\sqrt{3}}{3}$CD=1，当DE∥AB时，DE⊥AC，先证明△ADE为等边三角形，再证明四边形ABDE为菱形，然后利用弧长公式计算此时$\widehat{AE}$的长度；
②讨论：当∠ADE=90°时，AE为直径，利用弧长公式可计算出此时$\widehat{AE}$的长度；当∠DAE=90°时，DE为直径，利用圆周角定理得到∠AOE=2∠ADE=60°，然后利用弧长公式可计算出此时$\widehat{AE}$的长度．

解答 （1）证明：连接OD，如图，
∵∠BAC=90°，点D为BC的中点，
∴DB=DA=DC，
∵∠B=60°，
∴△ABD为等边三角形，
∴∠DAB=∠ADB=60°，∠DAC=∠C=30°，
而OA=OD，
∴∠ODA=∠OAD=30°，
∴∠ODB=60°+30°=90°，
∴OD⊥BC，
∴BD是⊙O的切线；
（2）解：①∵△ABD为等边三角形，
∴AB=BD=AD=CD=$\sqrt{3}$，
在Rt△ODC中，OD=$\frac{\sqrt{3}}{3}$CD=1，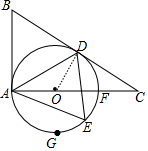
当DE∥AB时，DE⊥AC，
∴AD=AE，
∵∠ADE=∠BAD=60°，
∴△ADE为等边三角形，
∴AD=AE=DE，∠ADE=60°，
∴∠AOE=2∠ADE=120°，
∴AB=BD=DE=AE，
∴四边形ABDE为菱形，
此时$\widehat{AE}$的长度=$\frac{120•π•1}{180}$=$\frac{2}{3}$π；
②当∠ADE=90°时，AE为直径，点E与点F重合，此时$\widehat{AE}$的长度=$\frac{180•π•1}{180}$=π；
当∠DAE=90°时，DE为直径，∠AOE=2∠ADE=60°，此时$\widehat{AE}$的长度=$\frac{60•π•1}{180}$=$\frac{1}{3}$π，
所以当$\widehat{AE}$的长度为$\frac{1}{3}$π或π时，△ADE是直角三角形．
故答案为$\frac{2}{3}$π；$\frac{1}{3}$π或π．

点评 本题考查了圆的综合题：熟练掌握垂径定理、圆周角定理、切线的判定方法和菱形的判定方法；灵活应用等边三角形的性质进行几何计算；记住弧长公式．