
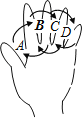
【题目】如图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始 数连续的正整数1,2,3,4…,当数到12时,对应的字母是_____;当字母C第201次出现时,恰好数到的数是_____.
【答案】B 603
【解析】
观察A→B→C→D→C→B→A→B→C→…可知:A→B→C→D→C→B,6个字母循环出现,用12除以6,余数是几就是第几个,整除是第6个,即可进行判断;
把A→B→C→D→C→B分为前后两组各3个,C分别出现一次,当次数为奇数则出现在第一组,偶数次出现在第二组,用出现的次数乘以3,再根据哪一组进行判断.
解:观察A→B→C→D→C→B→A→B→C→…可知:A→B→C→D→C→B,6个字母循环出现,
12÷6=2,所以:数到12时,对应的字母是:B,
201次,C应在A→B→C一组内,201×3=603,
所以:字母C第201次出现时,恰好数到的数是603.
故答案为:B,603.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOB=90°,∠COD=20°,OM平分∠AOC,ON平分∠BOD.
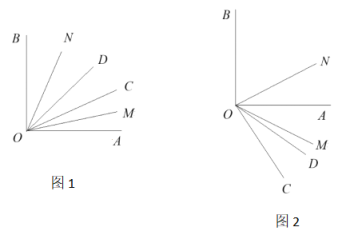
(1)如图1,∠COD在∠AOB内部,且∠AOC=30°.则∠MON的大小为 .
(2)如图1,∠COD在∠AOB内部,若∠AOC的度数未知,是否能求出∠MON的大小,若能,写出你的解答过程;若不能,说明理由.
(3)如图2,∠COD在∠AOB外部(OM在OD上方,∠BOC![]() 180°),试求出∠MON的大小.
180°),试求出∠MON的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李昨天下午的营运全是在东西走向的人民大街上进行的,如果规定向东为正,向西为负,他这天下午行车里程如下:+15,-2,+3,-1,+10,-3,-2.
(1)将最后一名乘客送往目的地时,小李距离下午出车时的出发点多远?
(2)若汽车耗油量为![]() ,这天下午小李共耗油多少L?
,这天下午小李共耗油多少L?
(3)小李所开的出租车按物价部门规定,起步价(不超过3km)5元,超过3km超过的部分每千米收费1元,小李这天下午收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列有理数:﹣(﹣3)、﹣4、0、+5、﹣![]()
(1)这些有理数中,整数有 个,非负数有 个.
(2)画数轴,并在数轴上表示这些有理数.
(3)把这些有理数用“<“号连接起来: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知R t△ABC,∠ABC=90°,以直角边AB为直径作O,交斜边AC于点D,连结BD.
(1)若AB=3,BC=4,求边BD的长;
(2)取BC的中点E,连结ED,试证明ED与⊙O相切.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市创建“绿色发展模范城市”,针对境内长江段两种主要污染源:生活污水和沿江工厂污染物排放,分别用“生活污水集中处理”(下称甲方案)和“沿江工厂转型升级”(下称乙方案)进行治理,若江水污染指数记为Q,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的Q值都以平均值n计算.第一年有40家工厂用乙方案治理,共使Q值降低了12.经过三年治理,境内长江水质明显改善.
(1)求n的值;
(2)从第二年起,每年用乙方案新治理的工厂数量比上一年都增加相同的百分数m,三年来用乙方案治理的工厂数量共190家,求m的值,并计算第二年用乙方案新治理的工厂数量;
(3)该市生活污水用甲方案治理,从第二年起,每年因此降低的Q值比上一年都增加个相同的数值a.在(2)的情况下,第二年,用乙方案所治理的工厂合计降低的Q值与当年因甲方案治理降低的Q值相等,第三年,用甲方案使Q值降低了39.5.求第一年用甲方案治理降低的Q值及a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数a,b,定义两种新运算“※”与“◎”,规定: a※b=a2+2ab,a◎b=|a+ b|-|a- b|,例如,2※(- 1)=22+2×2×(-1)=0,(- 2) ※3=|-2+3|-| - 2-3|= -4.![]() b c
b c
(1)计算(- 3) ※2的值;
(2)若a, b在数轴上的位置如图所示,化简a◎b;
![]()
(3)若(-2) ※x=2◎(- 4)+ 3x,求x的值:
(4)对于任意有理数m,n,请你定义一种新运算“★” ,使得(-3) ★5 = 4,直接写出你定义的运算:m★n=_ (用含m,n的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com