
 如图,已知点A的坐标为(5,0),直线y=x+b(b≥0)与y轴交于点B,连接AB,∠α=75°,则b的值为$\frac{5\sqrt{3}}{3}$.
如图,已知点A的坐标为(5,0),直线y=x+b(b≥0)与y轴交于点B,连接AB,∠α=75°,则b的值为$\frac{5\sqrt{3}}{3}$. 分析 设直线y=x+b(b≥0)与x轴交于点C,由直线BC的解析式可得出∠BCO=45°,结合∠α=75°可得出∠BAO=30°,通过解含30度角的直角三角形即可得出b值.
解答 解:设直线y=x+b(b≥0)与x轴交于点C,如图所示.
∵直线BC的解析式为y=x+b,
∴∠BCO=45°.
∵∠α=75°,
∴∠BAO=30°.
当x=0时,y=x+b=b.
在Rt△ABO中,∠BAO=30°,OB=b,OA=5,
∴AB=2b,
∴OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{3}$b=5,
∴b=$\frac{5\sqrt{3}}{3}$.
故答案为:$\frac{5\sqrt{3}}{3}$.
点评 本题考查了一次函数图象上点的坐标特征以及解含30度角的直角三角形,通过解含30度角的直角三角形求出b值是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,直线y=$\frac{1}{2}$x+1与y轴交于A点,过点A的抛物线y=-$\frac{5}{4}$x2+bx+c与直线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
如图,直线y=$\frac{1}{2}$x+1与y轴交于A点,过点A的抛物线y=-$\frac{5}{4}$x2+bx+c与直线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
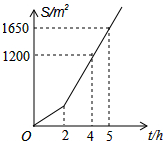 明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是150m2.
明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是150m2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是( )
如图,半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是( )| A. | 18$\sqrt{3}$-6π | B. | 4$\sqrt{3}$-$\frac{4}{3}$π | C. | 9$\sqrt{3}$-$\frac{9}{2}$π | D. | 2$\sqrt{3}$-$\frac{2}{3}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
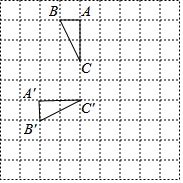 如图,在边长为1的小正方形网格中,将△ABC绕某点旋转到△A'B'C'的位置,则点B运动的最短路径长为$\frac{\sqrt{13}}{2}$π.
如图,在边长为1的小正方形网格中,将△ABC绕某点旋转到△A'B'C'的位置,则点B运动的最短路径长为$\frac{\sqrt{13}}{2}$π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com