
 已知△ABC为等边三角形,D、E、F分别为AB边、AC边、BC边的中点,且小三角形EDF的面积为6cm2,将△ABC沿DE、EF、DF折叠后能拼成一个什么立体图形?拼成的立体图形的表面积是多少?
已知△ABC为等边三角形,D、E、F分别为AB边、AC边、BC边的中点,且小三角形EDF的面积为6cm2,将△ABC沿DE、EF、DF折叠后能拼成一个什么立体图形?拼成的立体图形的表面积是多少? 科目:初中数学 来源: 题型:解答题
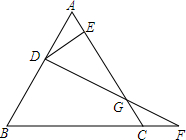 如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.
如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校七年级3月月考数学试卷(解析版) 题型:单选题
如果一个角是60°,那么 它的余角的度数是( )
它的余角的度数是( )
A. 30° B. 60° C. 90° D. 120°
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省瑞安市五校联考八年级下学期第一次月考数学试卷(解析版) 题型:解答题
某小区有一块长18米,宽8米的长方形空地,计划在其中修建两块相同的长方形花圃.为方便游人观赏,准备在花圃周边修建如图所示的“两横三纵”人行通道,其中横向人行通道的宽度是纵向人行通道宽度的一半.设纵向人行通道的宽度为 米,当
米,当 为何值时,花圃的面积之和为72米
为何值时,花圃的面积之和为72米 ?
?

查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省瑞安市五校联考八年级下学期第一次月考数学试卷(解析版) 题型:单选题
把一元二次方程 化成一般形式
化成一般形式 (a≠0),其中a、b、c 的值分别为( )
(a≠0),其中a、b、c 的值分别为( )
A. 2、3、﹣1 B. 2、﹣3、1 C. 2、﹣3、﹣1 D. 2、3、1
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com