
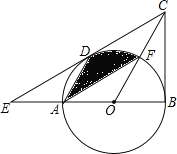
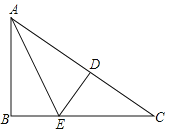
【题目】如图,在△BCE中,点A时边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)根据已知条件易证△CDO≌△CBO,即可得∠CBO=∠CDO=90°,所以CB是⊙O的切线;(2)根据条件证明△ADG≌△FOG,可得S△ADG=S△FOG,再由S阴=S扇形ODF,利用扇形面积公式计算即可.
试题解析:(1)证明:连接OD,与AF相交于点G,
∵CE与⊙O相切于点D,
∴OD⊥CE,
∴∠CDO=90°,
∵AD∥OC,
∴∠ADO=∠1,∠DAO=∠2,
∵OA=OD,
∴∠ADO=∠DAO,
∴∠1=∠2,
在△CDO和△CBO中,
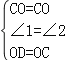 ,
,
∴△CDO≌△CBO,
∴∠CBO=∠CDO=90°,
∴CB是⊙O的切线.
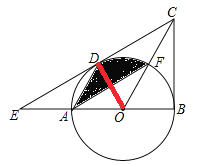
(2)由(1)可知∠3=∠BCO,∠1=∠2,
∵∠ECB=60°,
∴∠3=![]() ∠ECB=30°,
∠ECB=30°,
∴∠1=∠2=60°,
∴∠4=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴AD=OD=OF,∵∠1=∠ADO,
在△ADG和△FOG中,
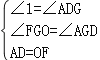 ,
,
∴△ADG≌△FOG,
∴S△ADG=S△FOG,
∵AB=6,
∴⊙O的半径r=3,
∴S阴=S扇形ODF=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A.两直线与第三条直线相交,同位角相等;
B.两直线与第三条直线相交,内错角相等
C.两直线平行,内错角相等;
D.两直线平行,同旁内角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() △ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,则EB=_____________.
△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,则EB=_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,AD∥BC,当满足下列条件时,四边形ABCD是平行四边形的是( ).
A.∠A+∠C=180°
B.∠B+∠D=180°
C.∠A+∠B=180°
D.∠A+∠D=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校2 000名师生对我市 “三创”工作(创国家园林城市、国家卫生城市、全国文明城市)的知晓情况,从中随机抽取了100名师生进行问卷调查,这项调查中的样本是( )
A. 2 000名师生对“三创”工作的知晓情况
B. 从中抽取的100名师生
C. 从中抽取的100名师生对“三创”工作的知晓情况
D. 100
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com