
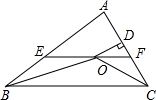
 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
分析 由在△ABC中,∠ABC和∠ACB的平分线相交于点O,根据角平分线的定义与三角形内角和定理,即可求得②∠BOC=90°+$\frac{1}{2}$∠A正确;由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出EF=BE+CF故①正确;由角平分线的性质得出点O到△ABC各边的距离相等,故③正确;由角平分线定理与三角形面积的求解方法,即可求得③设OD=m,AE+AF=n,则S△AEF=$\frac{1}{2}$mn,故④错误.
解答 解:∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°-$\frac{1}{2}$∠A,
∴∠BOC=180°-(∠OBC+∠OCB)=90°+$\frac{1}{2}$∠A;故②正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
故①正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,
∴S△AEF=S△AOE+S△AOF=$\frac{1}{2}$AE•OM+$\frac{1}{2}$AF•OD=$\frac{1}{2}$OD•(AE+AF)=$\frac{1}{2}$mn;故④错误;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴点O到△ABC各边的距离相等,故③正确.
故选A.
点评 此题考查了角平分线的定义与性质,等腰三角形的判定与性质.此题难度适中,解题的关键是注意数形结合思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 0.40064×104 | B. | 4.0064×103 | C. | 4.0064×104 | D. | 40.064×102 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.3×106 | B. | 3×105 | C. | 3×106 | D. | 30×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.56×101 | B. | 3.56×104 | C. | 3.56×105 | D. | 35.6×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC=200m,∠CAB=54°,∠CBA=30°.
为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC=200m,∠CAB=54°,∠CBA=30°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
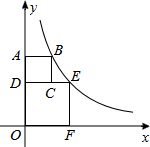 如图,在平面直角坐标系xOy中,四边形ODEF和四边形ABCD都是正方形,点F在x轴的正半轴上,点C在边DE上,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象过点B,E.若AB=2,则k的值为6+2$\sqrt{5}$.
如图,在平面直角坐标系xOy中,四边形ODEF和四边形ABCD都是正方形,点F在x轴的正半轴上,点C在边DE上,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象过点B,E.若AB=2,则k的值为6+2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
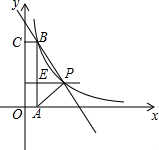 如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,函数y=$\frac{k}{x}$的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).
如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,函数y=$\frac{k}{x}$的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com