
【题目】在平面直角坐标系![]() 中,点
中,点![]() 为
为![]() 轴上的动点,点
轴上的动点,点![]() 为
为![]() 轴上方的动点,连接
轴上方的动点,连接![]() ,
,![]() ,
,![]() .
.
(1)如图1,当点![]() 在
在![]() 轴上,且满足
轴上,且满足![]() 的角平分线与
的角平分线与![]() 的角平分线交于点
的角平分线交于点![]() ,请直接写出
,请直接写出![]() 的度数;
的度数;

(2)如图2,当点![]() 在
在![]() 轴上,
轴上,![]() 的角平分线与
的角平分线与![]() 的角平分线交于点
的角平分线交于点![]() ,点
,点![]() 在
在![]() 的延长线上,且满足
的延长线上,且满足![]() ,求
,求![]() ;
;

(3)如图3,当点![]() 在第一象限内,点
在第一象限内,点![]() 是
是![]() 内一点,点
内一点,点![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 上一点,满足:
上一点,满足:![]() ,
,![]() ,
,![]() .
.

以下结论:①![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() .
.
正确的是:________.(请填写正确结论序号,并选择一个正确的结论证明,简写证明过程).
【答案】(1)135°,(2)2;(3)②③④,理由见详解
【解析】
(1)根据三角形内角和定理(三角形的内角和是180°)和角平分线定理可求∠P的度数,进而得到答案;
(2)根据三角形外角的性质和角平分线定理可求解,进而可以得到答案;
(3)过点P作PF⊥OA于点F,过点P作PE⊥OB于点E,根据全等三角形的性质和角平分线性质,可求解.
解:(1) ∵∠AOB=90°,
∴∠OAB+∠OBA=90°,
∵AP平分∠OAB,BP平分∠OBA,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2) ∵BC平分∠ABO,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3) 如图,连接OP,过点P作PF⊥OA于点F,过点P作PE⊥OB于点E,

∵∠ONP+∠OMP=180°,且∠OMP+∠PMF=180°,
∴∠PNO=∠PMF,且PN=PM,∠PEO=∠PFO=90°
∴△PEN≌△PMF(AAS)
∴PE=PF,且PE⊥OB,PF⊥OA
∴OP平分∠AOB,
如上图,作BH平分∠OBA,交OP延长线于点H,连接AH,
∵BH平分∠OBA,OH平分∠BOA,
∴AH平分∠OAB
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点H与点P重合,
∴AP平分∠OAB;BP平分∠OBA,
故②③正确,
∵PE=PF,OP=OP
∴Rt△OPE≌Rt△OPF(HL)
∴OE=OF,且OM<OF=OE<ON
故①错误
如上图,在AB上截取AQ=AM,
∵AM=AQ,∠OAP=∠BAP,AP=AP
∴△MAP≌△QAP(SAS),
∴∠PMA=∠PQA,
∴∠ONP=∠AQP,
∴∠BNP=∠BQP,且BP=BP,∠OBP=∠ABP,
∴△BPN≌△BPQ(AAS),
∴BN=BQ,
∴AB=AQ+BQ=AM+BN,
故④正确
故答案为:②③④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)作出△ABC绕点A顺时针方向旋转90°后得到的△A1B1C1,并写出C1点的坐标 ;
(2)作出△ABC关于原点O成中心对称的△A2B2C2,并求出△ABC的面积 .

查看答案和解析>>
科目:初中数学 来源: 题型:
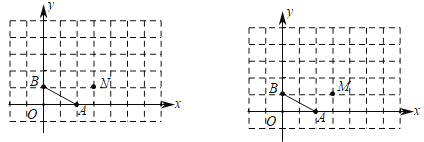
【题目】如图,点![]() 的坐标分别为
的坐标分别为![]() ,将线段
,将线段![]() 直接平移到
直接平移到![]() ,使点
,使点![]() 移至点
移至点![]() 的位置,点
的位置,点![]() 移至点
移至点![]() 的位置,设平移过程中线段
的位置,设平移过程中线段![]() 扫过的面积为
扫过的面积为![]() ,
,
(1)如图1,若点![]() 的坐标是
的坐标是![]() ,则点
,则点![]() 的坐标为_____________,请画出平移后的线段
的坐标为_____________,请画出平移后的线段![]() ;
;
(2)如图2,若点![]() 的坐标是
的坐标是![]() ,请画出平移后的线段
,请画出平移后的线段![]() ,则
,则![]() 的值为_____________;
的值为_____________;
(3)若![]() ,且点
,且点![]() 在坐标轴上,请直接写出所有满足条件的
在坐标轴上,请直接写出所有满足条件的![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
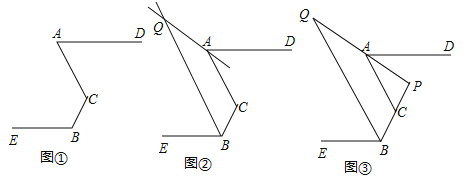
【题目】如图,已知:点![]() 不在同一条直线,
不在同一条直线,![]() .
.
(1)求证:![]() .
.
(2)如图②,![]() 分别为
分别为![]() 的平分线所在直线,试探究
的平分线所在直线,试探究![]() 与
与![]() 的数量关系;
的数量关系;
(3)如图③,在(2)的前提下,且有![]() ,直线
,直线![]() 交于点
交于点![]() ,
,![]() ,请直接写出
,请直接写出![]() ______________.
______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的学习材料(研学问题),尝试解决问题:
(a)某学习小组在学习时遇到如下问题:如图①,在Rt△ABC中,∠C=90°,D为边BC上一点,DA=DB,E为AD延长线上一点,∠AEB=120°,猜想BC、EA、EB的数量关系,并证明结论.大家经探究发现:过点B作BF⊥AE交AE的延长线于F,如图②所示,构造全等三角形使问题容易求解,请写出解答过程.
(b)参考上述思考问题的方法,解答下列问题:
如图③,等腰△ABC中,AB=AC,H为AC上一点,在BC的延长线上顺次取点E、F,在CB的延长线上取点BD,使EF=DB,过点E作EG∥AC交DH的延长线于点G,连接AF,若∠HDF+∠F=∠BAC.
(1)探究∠BAF与∠CHG的数量关系;
(2)请在图中找出一条和线段AF相等的线段,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )

A. ∠D=∠C B. BD=AC C. ∠CAD=∠DBC D. AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图象中所反映的过程是:小敏从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中![]() 表示时间,
表示时间,![]() 表示小敏离家的距离,根据图象提供的信息,以下说法错误的是( )
表示小敏离家的距离,根据图象提供的信息,以下说法错误的是( )
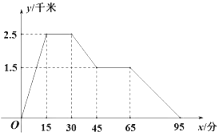
A. 体育场离小敏家2.5千米B. 体育场离早餐店4千米
C. 小敏在体育场锻炼了15分钟D. 小敏从早餐店回到家用时30分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
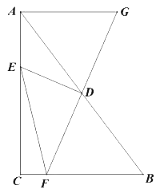
【题目】如图,在△ABC中,D是边AB的中点,E是边AC上一动点,连结DE,过点D作DF⊥DE交边BC于点F(点F与点B、C不重合),延长FD到点G,使DG=DF,连结EF、AG.已知AB=10,BC=6,AC=8.
(1)求证:△ADG≌△BDF;
(2)请你连结EG,并求证:EF=EG;
(3)设AE=![]() ,CF=
,CF=![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(4)求线段EF长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,线段AB,利用无刻度的直尺和圆规,作一个满足条件的△ABC:①△ABC为直角三角形;②tan∠A= ![]() .(注:不要求写作法,但保留作图痕迹)
.(注:不要求写作法,但保留作图痕迹)![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com