练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，从点发出一束光，经x轴反射，过点，则这束光从点A到点B所经过的路径的长为________.

    【答案】５

    【解析】

    先过点B作BD⊥x轴于D，再由A、B的坐标确定，即可得OA,BD,OD的长度，由题意可证得△AOC∽△BDC，根据相似三角形的对应边成比例，即可求解.

    解：如图，

    过点B作BD⊥x轴于D，

    ∵A（0，2），B（5，3），

    ∴OA=2，BD=3，OD=5，

    由反射定律可得：∠ACO=∠BCD，

    又∵∠AOC=∠BDC=90°

    ∴△AOC∽△BDC，

    ∴OA：BD=OC：DC=AC：BC=2：3，

    ∴OC=2，OD=3

    在Rt△BCD中，CD=3，BD=３

    ∴BC＝＝

    又∵AC：BC=2：3

    ∴AC＝

    ∴AC+BC＝5

    ..故选：5.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校学生会为了解本校学生每天体育锻炼所用时间情况，采用问卷的方式对一部分学生进行调查确定调查对象时，大家提出以下几种方案：（A）对各班体育委员进行调査；（B）对某班的全体学生进行调查；（C）从全校每班随机抽5名学生进行调查在问卷调查时，每位被调查的学都选择了问卷中适合自己的十个时间段，学生会将收集到的数据整理后续制成如下的统计表：

    被调查的学生每天体育锻炼所用时间统计表

    组别

    时间x（小时）

    频数

    一

    0≤x≤0.5

    15

    二

    0.6＜x≤1

    27

    三

    1＜x≤1.5

    38

    四

    1.5＜x≤2

    13

    五

    x＞2

    7

    （1）为了使收集到的数据具有代表性，学生会在确定调查对象时选择了方案　 　（填A、B或C）；

    （2）被调查的学生每天体育锻炼所用时间的中位数落在　 　组；

    （3）根据以上统计结果，估计该校900名学生中每天体育锻炼时间不超过0.5小时的人数，并根据你计算的结果提出一条合理化建议．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某届世界杯的小组比赛规则：四个球队进行单循环比赛（每两队赛一场），胜一场得3分，平一场得1分，负一场得0分.某小组比赛结束后，甲、乙、丙、丁四队分别获得第一、二、三、四名，各队的总得分恰好是四个连续奇数，则与乙打平的球队是（ ）

    A. 甲 B. 甲与丁 C. 丙 D. 丙与丁

    查看答案和解析>>

    科目：初中数学 来源： 题型：

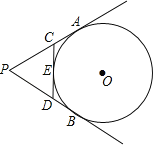
    【题目】如图，PA，PB切⊙O于A、B两点，CD切⊙O于点E，交PA，PB于C，D．若⊙O的半径为r，△PCD的周长等于3r，则tan∠APB的值是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

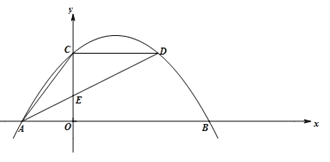
    【题目】如图，已知抛物线经过A（－3，0）、B（8，0）、C（0，4）三点，点D是抛物线上的动点，连结AD与y轴相交于点E，连结AC，CD．

    （1）求抛物线所对应的函数表达式；

    （2）当AD平分∠CAB时．

    ①求直线AD所对应的函数表达式；

    ②设P是x轴上的一个动点，若△PAD与△CAD相似，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

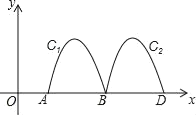
    【题目】如图，抛物线y＝﹣x2+4x﹣3与x轴交于点A、B，把抛物线在x轴及其上方的部分记作C1，将C1向右平移得到C2，C2与x轴交于B、D两点．若直线y＝kx﹣k与C1、C2共有3个不同的交点，则k的最大值是（　　）

    A.B.2﹣6C.6+4D.6﹣4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线经过坐标原点，与轴的另一个交点为，且顶点坐标为.

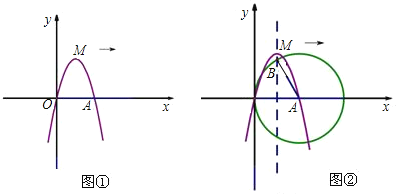
    （1）求抛物线解析式.

    （2）将抛物线向右平移个单位，所得抛物线与轴交于两点，与原抛物线交于点，设的面积为，求关于的函数关系式.

    （3）如图②，以点为圈心，以线段为半径画圆，交抛物线的对称轴于点，连结，若将抛物线向右平移个单位后，点的对应点为，点的对应点为，且满足四边形为菱形，平移后的抛物线的对称轴与菱形的对角线交于点问：在轴上是否存在一点，使得以，为顶点的三角形与相似？若存在，求出F点坐标，若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

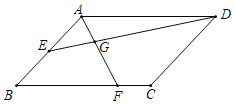
    【题目】如图，平行四边形ABCD的边长AD＝3，AB＝2，∠BAD＝120°，E为AB的中点，F在边BC上，且BF＝2FC．AF与DE交于点G，则AG的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线与轴交于点，与轴交于点，抛物线经过、两点．

    求抛物线的解析式；

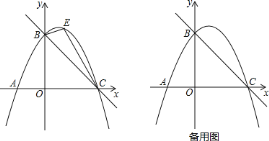
    如图，点是直线上方抛物线上的一动点，当面积最大时，请求出点的坐标和面积的最大值？

    在的结论下，过点作轴的平行线交直线于点，连接，点是抛物线对称轴上的动点，在抛物线上是否存在点，使得以、、、为顶点的四边形是平行四边形？如果存在，请直接写出点的坐标；如果不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案