
 如图,P是线段AB上异于端点的动点,且AB=6,分别以AP、BP为边,在AB的同侧作等边△APM和等边△BPN,则△MNP外接圆半径的最小值为$\sqrt{3}$.
如图,P是线段AB上异于端点的动点,且AB=6,分别以AP、BP为边,在AB的同侧作等边△APM和等边△BPN,则△MNP外接圆半径的最小值为$\sqrt{3}$. 分析 分别作∠A与∠B角平分线,交点为O.由三线合一可知AP与BP为PM、PN垂直平分线;再由垂径定理可知圆心O在PM、PN垂直平分线上,即圆心O是一个定点,连OP,若半径OP最短,则OP⊥AB,由△AOB为底边6,底角30°的等腰三角形,由此即可解决问题.
解答 解: 分别作∠A与∠B角平分线,交点为O,连接OP,
分别作∠A与∠B角平分线,交点为O,连接OP,
∵△AMP和△NPB都是等边三角形,
∴AO与BO为PM、PN垂直平分线.
∵圆心O在PM、PN垂直平分线上,即圆心O是一个定点,
若半径OP最短,则OP⊥AB.
又∵∠OAP=∠OBP=30°,AB=3,
∴OA=OB,
∴AP=BP=3,
∴在直角△AOP中,OP=AP•tan∠OAP=3×tan30°=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查了圆的综合题.需要掌握等边三角形的“三线合一”的性质,三角形的外接圆圆心为三角形的垂心,点到直线的距离垂线段最短以及解直角三角形等知识点,注意数形结合数学思想的应用.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
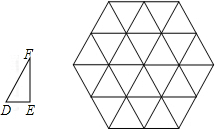 如图,△DEF的边长分别为1,$\sqrt{3}$,2,正六边形网格是由24个边长为2的正三角形组成,选择格点为顶点画△ABC,使得△ABC∽△DEF.如果相似比$\frac{AB}{DE}$=k,那么k的值可以是2,2$\sqrt{3}$,4.
如图,△DEF的边长分别为1,$\sqrt{3}$,2,正六边形网格是由24个边长为2的正三角形组成,选择格点为顶点画△ABC,使得△ABC∽△DEF.如果相似比$\frac{AB}{DE}$=k,那么k的值可以是2,2$\sqrt{3}$,4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 函数值随自变量的增大而减小 | |
| B. | 函数的图象不经过第三象限 | |
| C. | 函数的图象与x轴的交点坐标是(0,4) | |
| D. | 函数的图象向下平移4个单位长度得y=-2x的图象 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AC⊥BC,AC=BC,点D是AB中点,过C、D的⊙O交AC、BC分别于E、F.若⊙O的半径为$\sqrt{3}$,AC=2+2$\sqrt{2}$,则△CEF的面积为( )
如图,AC⊥BC,AC=BC,点D是AB中点,过C、D的⊙O交AC、BC分别于E、F.若⊙O的半径为$\sqrt{3}$,AC=2+2$\sqrt{2}$,则△CEF的面积为( )| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $2+\sqrt{2}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com