
【题目】如图,抛物线![]() (a≠0)与x轴交于点A(﹣5,0)和点B(3,0),与y轴交于点C.
(a≠0)与x轴交于点A(﹣5,0)和点B(3,0),与y轴交于点C.
(1)求该抛物线的解析式;
(2)若点E为x轴下方抛物线上的一动点,当S△ABE=S△ABC时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在点P,使∠BAP=∠CAE?若存在,求出点P的横坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)E(﹣2,﹣5);(3)
;(2)E(﹣2,﹣5);(3)![]() 或
或![]() .
.
【解析】
试题分析:(1)把A、B两点的坐标代入,利用待定系数法可求得抛物线的解析式;
(2)当S△ABE=S△ABC时,可知E点和C点的纵坐标相同,可求得E点坐标;
(3)在△CAE中,过E作ED⊥AC于点D,可求得ED和AD的长度,设出点P坐标,过P作PQ⊥x轴于点Q,由条件可知△EDA∽△PQA,利用相似三角形的对应边可得到关于P点坐标的方程,可求得P点坐标.
试题解析:(1)把A、B两点坐标代入解析式![]() ,可得:
,可得:![]() ,解得:
,解得:![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ;
;
(2)在![]() 中,令x=0可得y=﹣5,∴C(0,﹣5),∵S△ABE=S△ABC,且E点在x轴下方,∴E点纵坐标和C点纵坐标相同,当y=﹣5时,代入可得
中,令x=0可得y=﹣5,∴C(0,﹣5),∵S△ABE=S△ABC,且E点在x轴下方,∴E点纵坐标和C点纵坐标相同,当y=﹣5时,代入可得![]() ,解得x=﹣2或x=0(舍去),∴E点坐标为(﹣2,﹣5);
,解得x=﹣2或x=0(舍去),∴E点坐标为(﹣2,﹣5);
(3)假设存在满足条件的P点,其坐标为(m,![]() ),如图,连接AP、CE、AE,过E作ED⊥AC于点D,过P作PQ⊥x轴于点Q,则AQ=AO+OQ=5+m,PQ=
),如图,连接AP、CE、AE,过E作ED⊥AC于点D,过P作PQ⊥x轴于点Q,则AQ=AO+OQ=5+m,PQ=![]() ,在Rt△AOC中,OA=OC=5,则AC=
,在Rt△AOC中,OA=OC=5,则AC=![]() ,∠ACO=∠DCE=45°,由(2)可得EC=2,在Rt△EDC中,可得DE=DC=
,∠ACO=∠DCE=45°,由(2)可得EC=2,在Rt△EDC中,可得DE=DC=![]() ,∴AD=AC﹣DC=
,∴AD=AC﹣DC=![]() =
=![]() .当∠BAP=∠CAE时,则△EDA∽△PQA,∴
.当∠BAP=∠CAE时,则△EDA∽△PQA,∴![]() ,即
,即 ,∴
,∴![]() 或
或![]() ;
;
①当![]() 时,整理可得
时,整理可得![]() ,解得m=
,解得m=![]() 或m=﹣5(与A点重合,舍去);
或m=﹣5(与A点重合,舍去);
②当![]() 时,整理可得
时,整理可得![]() ,解得m=
,解得m=![]() 或m=﹣5(与A点重合,舍去),∴存在满足条件的点P,其横坐标为
或m=﹣5(与A点重合,舍去),∴存在满足条件的点P,其横坐标为![]() 或
或![]() .
.



 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,线段AD、FC、EB两两相交,连接AB、CD、EF,则∠A+∠B+∠C+∠D+∠E+∠F=( ) 
A.360°
B.240°
C.200°
D.180°
查看答案和解析>>
科目:初中数学 来源: 题型:
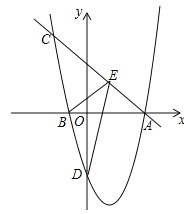
【题目】如图,抛物线![]() (a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
(a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
(1)求此抛物线的解析式;
(2)在直线AC上有一动点E,当点E在某个位置时,使△BDE的周长最小,求此时E点坐标;
(3)当动点E在直线AC与抛物线围成的封闭线A→C→B→D→A上运动时,是否存在使△BDE为直角三角形的情况,若存在,请直接写出符合要求的E点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上. 
(1)图中的全等三角形有;
(2)从你找到的全等三角形中选出其中一对加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A、∠B、∠C的对边分别是a、b、c,AB=8,BC=15,CA=17,则下列结论不正确的是( )
A.△ABC是直角三角形,且AC为斜边
B.△ABC是直角三角形,且∠ABC=90°
C.△ABC的面积是60
D.△ABC是直角三角形,且∠A=60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com