
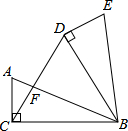
 如图所示,在△ABC=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F.
如图所示,在△ABC=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F.分析 (1)根据旋转角的定义进行解答;
(2)根据旋转的性质得到∠CBD=60°,BC=BD,然后根据等边三角形的判定方法判断△BCD是等边三角形,则等边三角形的三条边相等;
(3)先根据勾股定理计算出AB=13cm,再利用三角形周长定义得到△ACF与△BDF的周长之和=AC+CD+AB+BD,接着由△BCD为等边三角形得到CD=BC=BD=12,于是计算出△ACF与△BDF的周长之和.
解答  解:(1)如图,∵将△ABC绕点B顺时针旋转60°,得到△BDE,
解:(1)如图,∵将△ABC绕点B顺时针旋转60°,得到△BDE,
∴∠ABE=60°;
(2)∵△ABC绕点B顺时针旋转60°,得到△BDE,
∴∠CBD=60°,BC=BD=12cm,
∴△BCD为等边三角形,
∴DC=BC=12cm;
(3)在Rt△ABC中,∵∠ACB=90°,AC=5cm,BC=12cm,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13(cm),
∵△ACF与△BDF的周长之和=AC+CF+AF+DF+BD+BF=AC+CD+AB+BD,
∵△BCD为等边三角形,
∴CD=BC=BD=12,
∴△ACF与△BDF的周长之和=5+12+13+12=42(cm).
点评 本题考查了三角形综合题,需要掌握旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.还需要熟悉勾股定理的应用,难度不大.


科目:初中数学 来源: 题型:解答题
| 运行区间 | 公布票价 | 学生票 | ||
| 上车站 | 下车站 | 一等座 | 二等座 | 二等座 |
| 长沙 | 井冈山 | 81(元) | 68(元) | 51(元) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 路程(千米) | 运费(元/吨.千米) | |||
| 甲仓库 | 乙仓库 | 甲仓库 | 乙仓库 | |
| A地 | 25 | 20 | 1 | 0.8 |
| B地 | 20 | 15 | 1.2 | 1.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
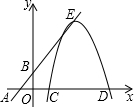 如图,一次函数y=x+2与x轴交于点A,与y轴交于点B,一抛物线的顶点在直线AB上,形状与函数y=-$\frac{1}{2}$x2图象相同,它与x轴分别交于点C、D(点C在点D的左侧),抛物线的顶点为点E.
如图,一次函数y=x+2与x轴交于点A,与y轴交于点B,一抛物线的顶点在直线AB上,形状与函数y=-$\frac{1}{2}$x2图象相同,它与x轴分别交于点C、D(点C在点D的左侧),抛物线的顶点为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
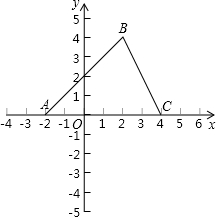 如图,在直角坐标系中,△ABC的顶点A(-2,0),B(2,4),C(4,0).
如图,在直角坐标系中,△ABC的顶点A(-2,0),B(2,4),C(4,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com