
 我市正在进行轻轨九号线的建设,为了缓解市区一些主要路段的交通拥堵现状,交警大队在主要路口设置了交通路况指示牌如图所示,小明在离指示牌3米的点A处测得指示牌顶端D点和底端E点的仰角分别为60°和30°,则路况指示牌DE的高度为( )
我市正在进行轻轨九号线的建设,为了缓解市区一些主要路段的交通拥堵现状,交警大队在主要路口设置了交通路况指示牌如图所示,小明在离指示牌3米的点A处测得指示牌顶端D点和底端E点的仰角分别为60°和30°,则路况指示牌DE的高度为( )| A. | 3-$\sqrt{3}$ | B. | 2$\sqrt{3}$-3 | C. | 2$\sqrt{3}$ | D. | 3+$\sqrt{3}$ |
分析 过A作AF⊥DC,交DC于点F,在直角三角形ADF中,利用锐角三角函数定义求出DF的长,在直角三角形AEF中,利用锐角三角函数定义求出EF的长,由DF-EF求出DE的长即可.
解答 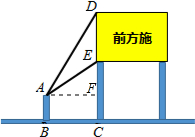 解:过A作AF⊥DC,交DC于点F,
解:过A作AF⊥DC,交DC于点F,
∴AF=BC=3米,
在Rt△ADF中,AF=3米,∠DAF=60°,
∴tan60°=$\frac{DF}{AF}$,即DF=3$\sqrt{3}$米,
在Rt△AEF中,AF=3米,∠EAF=30°,
∴tan30°=$\frac{EF}{AF}$,即EF=$\sqrt{3}$米,
则DE=DF-EF=3$\sqrt{3}$-$\sqrt{3}$=2$\sqrt{3}$米,
故选C
点评 此题考查了解直角三角形的应用-仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
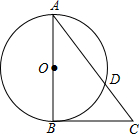 如图,△ABC是Rt△,∠ABC=90°,以AB为直径的⊙O交AC于D,⊙O的半径为5,$tanA=\frac{3}{4}$.
如图,△ABC是Rt△,∠ABC=90°,以AB为直径的⊙O交AC于D,⊙O的半径为5,$tanA=\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=AC=a,BC=b(a>b).在△ABC内依次作∠CBD=∠A,∠DCE=∠CBD,∠EDF=∠DCE,则EF等于$\frac{{b}^{4}}{{a}^{3}}$.
如图,在△ABC中,AB=AC=a,BC=b(a>b).在△ABC内依次作∠CBD=∠A,∠DCE=∠CBD,∠EDF=∠DCE,则EF等于$\frac{{b}^{4}}{{a}^{3}}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=8,则cosB的值是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=8,则cosB的值是( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com