
【题目】已知:如图①,在平面直角坐标系xOy中,A(0,5),C( ![]() ,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF.
,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF.
(1)求AF和OF的长;
(2)如图②,将△OAF绕点O顺时针旋转一个角α(0°<α<180°),记旋转中的△OAF为△OA′F′,在旋转过程中,设A′F′所在的直线与线段AD交于点P,与线段OD交于点Q,是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时点P坐标;若不存在,请说明理由.

【答案】
(1)解:如图①

∵OA=5,AD=OC= ![]() ,
,
由勾股定理可求.OD= ![]() ,
,
∵AE×OD=AO×AD,
∴AE=4,
∴OE= ![]() =3,
=3,
∵点F是点E关于y轴的对称点,
∴AF=AE=4,OF=OE=3
(2)解:如图②

若PD=PQ,
易得∠1=∠2=∠3,
∵∠1=∠A′,
∴∠3=∠A′,
∴OQ=OA′=5,
∴DQ= ![]() ,
,
过点P作PH⊥DQ,
∴ ![]() ,
,
∵cos∠1= ![]() ,
,
∴DP= ![]() ,
,
∴AP= ![]() ,
,
∴此时点P的坐标为( ![]() ,5);
,5);
如图③

∵点P在线段AD上,
∴∠1>∠PDQ,
∴QP,QD不会相等;
如图③,
若DP=DQ,
易得,∠1=∠2=∠3=∠4,
∵∠3=∠5+∠A′,∠A′=∠COD,
∴∠4=∠A′OQ,
∴A′Q=A′O=5,
∴F′Q=5﹣4=1,
∴OQ= ![]() ,
,
∴DP=DQ= ![]() ﹣
﹣ ![]() ,
,
∴AP=AD﹣DP= ![]() ﹣
﹣ ![]() ,
,
∴此时点P的坐标为:( ![]() ﹣
﹣ ![]() ,5)
,5)
【解析】(1)运用勾股定理和面积相等法结合轴对称性质即可求解;(2)画出图形,根据PQ=PD,PD=DQ结合平行线的性质,对顶角相等和角的等量代换,运用勾股定理即可求解.
【考点精析】掌握相似三角形的应用是解答本题的根本,需要知道测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球2个,蓝球1个,现在从中任意摸出一个红球的概率为 ![]() .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B. 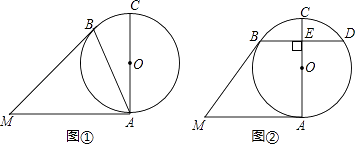
(1)如图①,若∠BAC=23°,求∠AMB的大小;
(2)如图②,过点B作BD∥MA,交AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC=30°,点D是BC边上的点,CD= 3,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,PE+PB的最小值 ______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=BC,点E是AC上一点,连接BE.
(1)若CB=4,BE=5,求AE的长;
(2)如图2,点D是线段BE延长线上一点,过点A作AF⊥BD于点F,连接CD、CF,当AF=DF时,求证:DC=BC;
小洁在遇到此问题时不知道怎么下手,秦老师提示他可以过点C作CH![]() CF,交DB于点H,先证明△AFC
CF,交DB于点H,先证明△AFC![]() △BHC,然后继续思考,并鼓励小洁把证明过程写出来.请你帮助小洁完成这个问题的证明过程.
△BHC,然后继续思考,并鼓励小洁把证明过程写出来.请你帮助小洁完成这个问题的证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C为圆上一点,AD和过点C的切线互相垂直,垂足为点D,AD交⊙O于点E.
(1)求证:AC平分∠BAD;
(2)若CD=3,AC=6,求图中阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是△ABC的外心,OD⊥BC,OE⊥AC,OF⊥AB,则OD:OE:OF等于( ).
A.a:b:c
B.![]()
C.sinA:sinB:sinC
D.cosA:cosB:cosC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com