
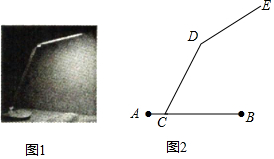
 如图1为放置在水平桌面上的某创意可折叠台灯的平面示意图,将其抽象成图2,量的∠DCB=60°,∠CDE=150°,灯杆CD的长为40cm,灯管DE的长为26cm,底座AB的厚度为2cm,不考虑其他因素,分别求出DE与水平卓,面(AB所在的直线)所成的夹角度数和台灯的高(点E到桌面的距离).(结果保留根号)
如图1为放置在水平桌面上的某创意可折叠台灯的平面示意图,将其抽象成图2,量的∠DCB=60°,∠CDE=150°,灯杆CD的长为40cm,灯管DE的长为26cm,底座AB的厚度为2cm,不考虑其他因素,分别求出DE与水平卓,面(AB所在的直线)所成的夹角度数和台灯的高(点E到桌面的距离).(结果保留根号) 分析 首先过点D作AB的平行线DM,根据平行线的性质求出∠CDM=120°,得出∠EDM的度数,即为DE与水平桌面(AB所在的直线)所成的夹角度数;再
作EF⊥DM于点F,DG⊥AB于点G,然后解直角三角形求出EF、DG的长,进而得出台灯的高.
解答  解:如图,过点D作AB的平行线DM,
解:如图,过点D作AB的平行线DM,
∵∠DCB=60°,
∴∠CDM=180°-∠DCB=120°,
∵∠CDE=150°,
∴∠EDM=∠CDE-∠CDM=150°-120°=30°,
即DE与水平桌面(AB所在的直线)所成的夹角度数为30°;
作EF⊥DM于点F,DG⊥AB于点G.
∵在直角△DEF中,∠EFD=90°,∠EDF=30°,DE=26cm,
∴EF=$\frac{1}{2}$DE=13cm,
∵在直角△CDG中,∠DGC=90°,∠DCG=60°,CD=40cm,
∴sin60°=$\frac{DG}{CD}$,
∴DG=CD•sin60°=40×$\frac{\sqrt{3}}{2}$=20$\sqrt{3}$cm,
∵底座AB的厚度为2cm,
∴点E到桌面的距离是:13+20$\sqrt{3}$+2=(15+20$\sqrt{3}$)cm.
答:台灯的高(点E到桌面的距离)为(15+20$\sqrt{3}$)cm.
点评 此题主要考查了解直角三角形的应用,根据已知求出EF,DG的长是解决问题的关键.


科目:初中数学 来源: 题型:解答题
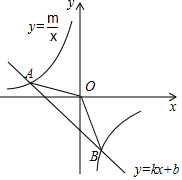 如图,已知A(-4,2)、B(a,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点;
如图,已知A(-4,2)、B(a,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
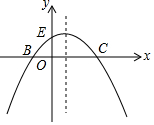 如图1,已知抛物线的方程C1:y=-$\frac{1}{m}$(x+2)(x-m)(m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
如图1,已知抛物线的方程C1:y=-$\frac{1}{m}$(x+2)(x-m)(m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ | B. | a3+a4=a7 | C. | a6÷a3=a3 | D. | (3a3)2=9a6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直径为1个单位长度的圆上一点A在数轴上的坐标为-1,该圆沿数轴向右滚动2014周,A点到达位置A′处,则A′的坐标为2014π-1.
如图,直径为1个单位长度的圆上一点A在数轴上的坐标为-1,该圆沿数轴向右滚动2014周,A点到达位置A′处,则A′的坐标为2014π-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com