
【题目】如图,已知△ABC是⊙O的内接三角形,D是OA延长线上的一点,连接DC,且∠B=∠D=30°,AC=4.
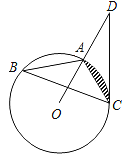
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)求阴影部分的面积.
【答案】(1)CD为⊙O的切线;(2)![]() π﹣4
π﹣4![]() .
.
【解析】
试题分析:(1)连结OC,如图,根据圆周角定理得到∠AOC=2∠B=60°,则利用三角形内角和可计算出∠OCD=90°,所以OC⊥CD,然后根据切线的判定定理可判断CD为⊙O的切线;
(2)先判断△AOC为等边三角形,则OA=AC=4,然后根据扇形面积公式和等边三角形的面积公式,利用S阴影部分=S扇形AOC﹣S△OAC进行计算.
解:(1)直线CD为⊙O的切线.理由如下:
连结OC,如图,
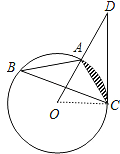
则∠AOC=2∠B=60°,
∵∠D=30°,
∴∠OCD=180°﹣30°﹣60°=90°,
∴OC⊥CD,
∴CD为⊙O的切线;
(2)∵OA=OC,∠AOC=60°,
∴△AOC为等边三角形,
∴OA=AC=4,
∴S阴影部分=S扇形AOC﹣S△OAC
=![]() ﹣
﹣![]() 42
42
=![]() π﹣4
π﹣4![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图,∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
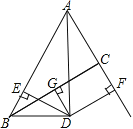
①求证:BE=CF;
②若AF=5,BC=6,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题的个数是( )
①同位角相等;②a,b,c是三条直线,若a⊥b,b⊥c,则a⊥c;③a,b,c是三条直线,若a∥b,b∥c,则a∥c;④过一点有且只有一条直线与已知直线平行.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s.
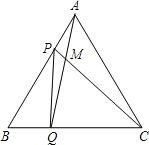
(1)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;
(2)请求出何时△PBQ是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在扇形统计图中,如果A部分扇面的面积是B部分扇面面积的2倍,则A部分扇面所对的圆心角是B部分扇面所对圆心角的( ).
A. 2倍 B. 1倍到2倍之间 C. 1.5倍 D. 无法计算
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年12月26日,南昌地铁一号线正式开通试运营.据统计,开通首日全天客流量累积近25万人次,数据25万可用科学记数法表示为( )
A.0.25×105 B.2.5×104 C.25×104 D.2.5×105
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com