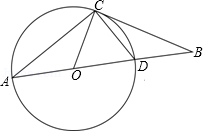
证明:(1)∵AD为⊙O的直径,∴∠ACD=90°。
又∵∠A=30°,OA=OC=OD,∴∠ACO=30°,∠ODC=∠OCD=60°。
又∵BC与⊙O切于C,∴∠OCB=90°,∴∠BCD=30°。∴∠B=30°。
∴∠BCD=∠B。∴BD=CD。
(2)∵∠A=∠ACO=∠BCD=∠B=30°,∴AC=BC。
在△AOC和△BDC中,∵∠A =∠B,AC=BC,∠ACO=∠BCD,
∴△AOC≌△BDC(ASA)。
(1)由AD为⊙O的直径,根据直径对的圆周角是直角,即可得∠ACD=90°,又由∠A=30°,OA=OC=OD,利用等边对等角与三角形外角的性质,即可求得∠ACO=30°,∠ODC=∠OCD=60°,又由BC与⊙O切于C点,根据切线的性质,即可求得∠B=∠BCD=30°,由等角对等边,即可证得BD=CD。
(2)由(1)可知∠A=∠ACO=∠BCD=∠B=30°,即可得AC=BC,然后由ASA,即可证得△AOC≌△CDB。