
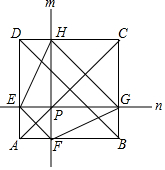
 ��ͼ��PΪ�߳�Ϊ4��������ABCD�ĶԽ���AC�϶��㣨����A��C�غϣ�����P��ֱ��m��n���ֱ���AD��ABƽ�У��������θ��߷ֱ���E��F��G��H���������ж��У�����ȷ���ǣ�������
��ͼ��PΪ�߳�Ϊ4��������ABCD�ĶԽ���AC�϶��㣨����A��C�غϣ�����P��ֱ��m��n���ֱ���AD��ABƽ�У��������θ��߷ֱ���E��F��G��H���������ж��У�����ȷ���ǣ�������| A�� | P��仯ʱ���ı���EFGH������ֲ��� | |
| B�� | P��仯ʱ��������DEFBGH��������ֵ12$\sqrt{2}$ | |
| C�� | ��Pλ��������ABCD������ʱ��DE=2 | |
| D�� | P��仯ʱ��������DEFBGH�ܳ����ֲ��� |
���� �����ų���֤��A��C��D��ȷ�����жϣ�
��� �⣺A����ȷ��P��仯ʱ���ı���EFGH������ֲ��䣮
���ɣ� S�ı���EFGH=S��PEH+S��PEF+S��PFG+S��PHG
S�ı���EFGH=S��PEH+S��PEF+S��PFG+S��PHG
=$\frac{1}{2}$S����DEPH+$\frac{1}{2}$S����AFPE+$\frac{1}{2}$S����BFPG+$\frac{1}{2}$S����PGCH
=$\frac{1}{2}$S������ABCD��
C����ȷ����Pλ��������ABCD������ʱ��DE=2��
D����ȷ����AP=x����PC=4$\sqrt{2}$-x��
��������DEFBGH�ܳ�=x+4$\sqrt{2}$-x+2•��4-$\frac{\sqrt{2}}{2}$x��+2•$\frac{\sqrt{2}}{2}$x=8+4$\sqrt{2}$=��ֵ��
��ѡ��B����
��ѡB��
���� ���⿼�������ε����ʡ�ƽ���ߵ����ʡ����ε����ʡ��ı��ε������֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����ų���������⣬�����п�ѡ�����е�ѹ���⣮


 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д� ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 4 | C�� | 3 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
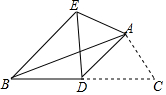 ��ͼ����֪AD�ǡ�ABC�����ߣ���ADC=45�㣬�ѡ�ADC��AD����ֱ�߶��ۣ���C���ڵ�E��λ�ã����EBC�Ķ�����
��ͼ����֪AD�ǡ�ABC�����ߣ���ADC=45�㣬�ѡ�ADC��AD����ֱ�߶��ۣ���C���ڵ�E��λ�ã����EBC�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 4 | C�� | 9 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5��10-7����2 | B�� | 5��10-8����2 | C�� | 2��106����2 | D�� | 2��107����2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
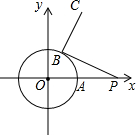 ��ƽ��ֱ������ϵ�У���ԭ��OΪԲ�ĵ�Բ����A��2��0����B��Ϊ��O������һ�㣬P��5��0��������BP�����߶�BP��B����ʱ����ת90�����߶�BC����B���A���������Բ��תһ�ܵĹ����У�C���˶�·����Ϊ��������
��ƽ��ֱ������ϵ�У���ԭ��OΪԲ�ĵ�Բ����A��2��0����B��Ϊ��O������һ�㣬P��5��0��������BP�����߶�BP��B����ʱ����ת90�����߶�BC����B���A���������Բ��תһ�ܵĹ����У�C���˶�·����Ϊ��������| A�� | 2$\sqrt{2}$�� | B�� | 4�� | C�� | 4$\sqrt{2}$�� | D�� | 6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
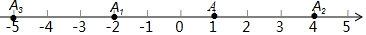 ��ͼ���������ϣ���A��ʾ1���ֽ���A�������������ƶ�����һ�ε�A�����ƶ�3����λ���ȵ����A1����2�δӵ�A1�����ƶ�6����λ���ȵ����A2����3�δӵ�A2�����ƶ�9����λ���ȵ����A3���������������ƶ����ɽ�����ȥ����n���ƶ������An�������An��ԭ��ľ��벻С��50����ôn����Сֵ��33��
��ͼ���������ϣ���A��ʾ1���ֽ���A�������������ƶ�����һ�ε�A�����ƶ�3����λ���ȵ����A1����2�δӵ�A1�����ƶ�6����λ���ȵ����A2����3�δӵ�A2�����ƶ�9����λ���ȵ����A3���������������ƶ����ɽ�����ȥ����n���ƶ������An�������An��ԭ��ľ��벻С��50����ôn����Сֵ��33���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
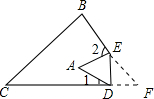 ��ͼ���ѡ�ABCֽƬ��DE�۵���ʹ��A�����ı���BCDE���ڲ������A���1����2�Ĺ�ϵΪ��������
��ͼ���ѡ�ABCֽƬ��DE�۵���ʹ��A�����ı���BCDE���ڲ������A���1����2�Ĺ�ϵΪ��������| A�� | ��A=��1+��2 | B�� | 3��A=2����1+��2�� | C�� | 3��A=2��1+��2 | D�� | 2��A=��1+��2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com