
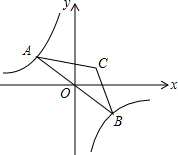
 如图,已知反比例函数y=-$\frac{1}{x}$的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为y=$\frac{1}{3x}$.
如图,已知反比例函数y=-$\frac{1}{x}$的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为y=$\frac{1}{3x}$. 分析 连接CO,过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,证明△AOD∽△OCE,根据相似三角形的性质求出△AOD和△OCE面积比,根据反比例函数图象上点的特征求出S△AOD,得到S△EOC,根据反比例函数比例系数k的几何意义求解.
解答 解:连接CO,过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,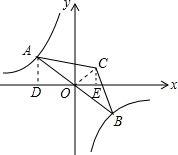
∵反比例函数y=-$\frac{1}{x}$的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,
∴CO⊥AB,∠CAB=30°,
则∠AOD+∠COE=90°,
∵∠DAO+∠AOD=90°,
∴∠DAO=∠COE,
又∵∠ADO=∠CEO=90°,
∴△AOD∽△OCE,
∴$\frac{AD}{EO}$=$\frac{OD}{CE}$=$\frac{OA}{OC}$=tan60°=$\sqrt{3}$,
∴$\frac{{S}_{△AOD}}{{S}_{△OCE}}$=($\sqrt{3}$)2=3,
∵点A是双曲线y=-$\frac{1}{x}$在第二象限分支上的一个动点,
∴S△AOD=$\frac{1}{2}$×|xy|=$\frac{1}{2}$,
∴S△OCE=$\frac{1}{6}$,即$\frac{1}{2}$×OE×CE=$\frac{1}{6}$,
∴OE×CE=$\frac{1}{3}$,
∴这个图象所对应的函数解析式为y=$\frac{1}{3x}$.
故答案为:y=$\frac{1}{3x}$.
点评 此题主要考查了反比例函数与一次函数的交点以及相似三角形的判定与性质,得出△AOD∽△OCE是解题关键.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
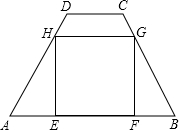 如图,在四边形ABCD中,AB∥CD,AB=15,CD=5,AD=BC=13,矩形EFGH内接于四边形ABCD中.
如图,在四边形ABCD中,AB∥CD,AB=15,CD=5,AD=BC=13,矩形EFGH内接于四边形ABCD中.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com