
【题目】如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,
且![]() .
.
(1)求证:∠BAE=∠CAD;
(2)求证:△ABE∽△ACD.

科目:初中数学 来源: 题型:
【题目】沿河岸有![]() ,
,![]() ,
,![]() 三个港口,甲、乙两船同时分别从
三个港口,甲、乙两船同时分别从![]() ,
,![]() 港口出发,匀速驶向
港口出发,匀速驶向![]() 港,最终到达
港,最终到达![]() 港.设甲、乙两船行驶
港.设甲、乙两船行驶![]() 后,与
后,与![]() 港的距离分别为
港的距离分别为![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 的函数关系如图所示.则:
的函数关系如图所示.则:
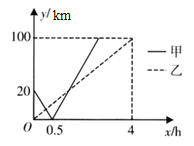
①从![]() 港到
港到![]() 港全程为______
港全程为______![]() ;
;
②如果两船相距小于![]() 能够相互望见,那么在甲船到达
能够相互望见,那么在甲船到达![]() 港前甲、乙两船可以相互望见时,
港前甲、乙两船可以相互望见时,![]() 的取值范围是______.
的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=62°,∠ACB=29°,求∠FGC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,过点D作AC的平行线交AB于点O,DE⊥AD交AB于点E.
(1)求证:点O是AE的中点;
(2)若点F是AC边上一点,且OF=OA,连接EF,如图2,判断EF与AC的位置关系,并说明理由;
(3)在(2)的条件下,试探究线段AE、AF、AC之间满足的等量关系,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本1.4有这样一道例题:

据此,一位同学提出问题:“用这根长22 cm的铁丝能否围成面积最大的矩形?若能围成,求出面积最大值;若不能围成,请说明理由.”请你完成该同学提出的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寒假即将到来,外出旅游的人数逐渐增多,对旅行包的需求也将增多,某店准备到生产厂家购买旅行包,该厂有甲、乙两种新型旅行包.若购进10个甲种旅行包和20个乙种旅行包共需5600元,若购进20个甲种旅行包和10个乙种旅行包共需5200元.
(1)甲、乙两种旅行包的进价分别是多少元?
(2)若该店恰好用了7000元购买旅行包;
①设该店购买了m个甲种旅行包,求该店购买乙种旅行包的个数;
②若该店将甲种旅行包的售价定为298元,乙种旅行包的售价定为325元,则当该店怎么样进货,才能获得最大利润,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如表
A种产品 | B种产品 | |
成本(万元/件) | 2 | 5 |
利润(万元/件) | 1 | 3 |
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少?
(2)若工厂计划投入资金不多于34万元,且获利多于14万元,问工厂有哪几种生产方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com