练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．图1、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，每个小正方形的顶点叫做格点．
    （1）在图1中画出等腰直角三角形MON，使点N在格点上，且∠MON=90°；
    （2）在图2中以格点为顶点画一个正方形ABCD，使正方形ABCD面积等于（1）中等腰直角三角形MON面积的4倍，并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形，且正方形ABCD面积没有剩余（画出一种即可）．

    分析 （1）过点O向线段OM作垂线，此直线与格点的交点为N，连接MN即可；
    （2）根据勾股定理画出图形即可．

    解答 解：（1）如图1所示；

    （2）如图2、3所示；

    点评 本题考查的是作图-应用与设计作图，熟知勾股定理是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

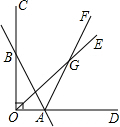    11．已知如图，直线AB与OC交于点B，与OD交于点A，射线OE和射线AF交于点G．
    （1）若∠COD=90°，OE平分∠BOA，AF平分∠BAD，∠OBA=36°求∠OGA的度数．
    （2）若∠COD＜90°，
    ①∠GOA=$\frac{1}{3}$∠BOA，∠GAD=$\frac{1}{3}$∠BAD，∠OBA=36°，求∠OGA的度数．
    ②将①中“∠OBA=36°”改为“∠OBA=β”，其余条件不变，则∠OGA=$\frac{β}{3}$（用含β的代数式表示）．
    （3）若∠COD＜90°，∠GOA=$\frac{1}{n}$∠BOA，∠GAD=$\frac{1}{n}$∠BAD，∠OBA=β°，则∠OGA=$\frac{β}{n}$．（含n、β的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图，AB是⊙O的直径，CD为⊙O的一条弦，CD⊥AB于点E，已知CD=4，AE=1，则⊙O的半径为$\frac{5}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．已知矩形的面积为10，长和宽分别为x和y，则y关于x的函数图象大致是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图所示，某数学活动小组选定测量小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30°，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°，若坡角∠FAE=30°，求大树的高度（结果保留整数，参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11，$\sqrt{3}$≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

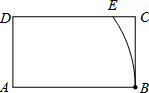    6．如图，在矩形ABCD中，AB=4，AD=2，以点A为圆心，AB长为半径画圆弧交边DC于点E，则$\widehat{BE}$的长度为$\frac{2}{3}π$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．已知不等式：①x-3＜0；②1＞3-x；③$\frac{x+1}{2}$-x＜$\frac{x-1}{2}$．从这3个不等式中任取2个构成不等式组，其中是否存在一个解集中只有一个整数解的不等式组？若存在，写出不等式组并求这个整数解；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

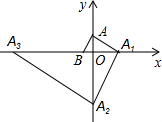    10．如图，在平面直角坐标系中，点A（0，$\sqrt{3}$）、B（-1，0），过点A作AB的垂线交x轴于点A1，过点A1作AA1的垂线交y轴于点A2，过点A2作A1A2的垂线交x轴于点A3…按此规律继续作下去，直至得到点A2015为止，则点A2015坐标为（-31008，0），．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

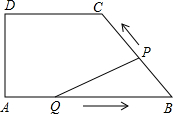    11．如图，在四边形ABCD中，DC∥AB，DA⊥AB，AD=4cm，DC=5cm，AB=8cm．如果点P由B点出发沿BC方向向点C匀速运动，同时点Q由A点出发沿AB方向向点B匀速运动，它们的速度均为1cm/s，当P点到达C点时，两点同时停止运动，连接PQ，设运动时间为t s，解答下列问题：
    （1）当t为何值时，P，Q两点同时停止运动？
    （2）设△PQB的面积为S，当t为何值时，S取得最大值，并求出最大值；
    （3）当△PQB为等腰三角形时，求t的值．

    查看答案和解析>>

    同步练习册答案