
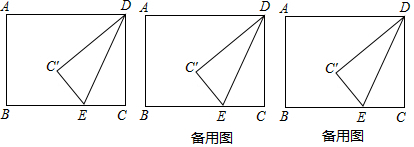
分析 (1)根据∠C=90°,BC=8,可得Rt△BCD中,BD=10,据此可得BC′=10-6=4.
(2)由折叠得,∠CED=∠C′ED,根据BC′∥DE,可得∠EC′B=∠C′ED,∠CED=∠C′BE,进而得到∠EC′B=∠C′EB,据此可得BE=C′E=EC=4;
(3)作AD的垂直平分线,交AD于点M,交BC于点N,分两种情况讨论:①当点C′在矩形内部时;②当点C′在矩形外部时,分别根据勾股定理,列出关于x的方程进行求解即可.
解答 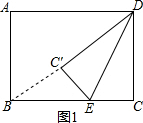 解:(1)如图1,由折叠可得DC'=DC=6,
解:(1)如图1,由折叠可得DC'=DC=6,
∵∠C=90°,BC=8,
∴Rt△BCD中,BD=10,
∴BC′=10-6=4.
故答案为4;
(2)如图2,由折叠得,∠CED=∠C′ED,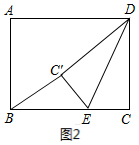
∵BC′∥DE,
∴∠EC′B=∠C′ED,∠CED=∠C′BE,
∴∠EC′B=∠C′EB,
∴BE=C′E=EC=4;
(3)作AD的垂直平分线,交AD于点M,交BC于点N,分两种情况讨论:
①当点C′在矩形内部时,如图3,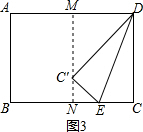
∵点C′在AD的垂直平分线上,
∴DM=4,
∵DC′=6,
∴由勾股定理得:MC′=2$\sqrt{5}$,
∴NC′=6-2$\sqrt{5}$,
设EC=x,则C′E=x,NE=4-x,
∵NC′2+NE2=C′E2,
∴(6-2$\sqrt{5}$)2+(4-x)2=x2,
解得:x=9-3$\sqrt{5}$,
即CE=9-3$\sqrt{5}$;
②当点C′在矩形外部时,如图4,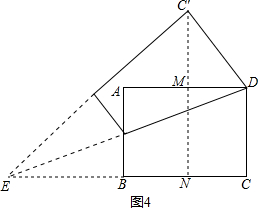
∵点C′在AD的垂直平分线上,
∴DM=4,
∵DC′=6,
∴由勾股定理得:MC′=2$\sqrt{5}$,
∴NC′=6+2$\sqrt{5}$,
设EC=y,则C′E=y,NE=y-4,
∵NC′2+NE2=C′E2,
∴(6+2$\sqrt{5}$)2+(y-4)2=y2,
解得:y=9+3$\sqrt{5}$,
即CE=9+3$\sqrt{5}$,
综上所述,CE的长为9±3$\sqrt{5}$.
点评 本题属于四边形综合题,主要考查了折叠的性质,矩形的性质,垂直平分线的性质以及勾股定理的综合应用.折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.解题时,常常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
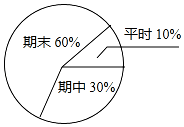 下面的表格是李刚同学一学期数学成绩的记录,根据表格提供的信息回答下面的问题
下面的表格是李刚同学一学期数学成绩的记录,根据表格提供的信息回答下面的问题 | 考试类别 | 平时 | 期中考试 | 期末考试 | |||
| 第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
| 成绩 | 88 | 86 | 90 | 92 | 90 | 96 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,函数y=kx与y=$\frac{m}{x}$的图象在第一象限内交于点A,过点A作AD垂直x轴于点D,且S△AOD=$\frac{3}{2}$.
如图,函数y=kx与y=$\frac{m}{x}$的图象在第一象限内交于点A,过点A作AD垂直x轴于点D,且S△AOD=$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A、B两点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,其中k>0,AC⊥y轴于点C,BD⊥x轴于点D,且AC=1
如图,A、B两点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,其中k>0,AC⊥y轴于点C,BD⊥x轴于点D,且AC=1查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com