
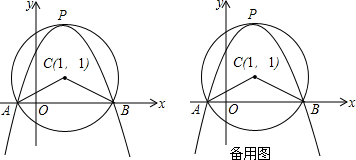
分析 (1)根据勾股定理求出AH和BH,根据C的坐标求出A、B的坐标即可;
(2)根据抛物线的顶点坐标设抛物线的顶点式,把B的坐标代入求出a即可;
(3)假设存在,根据平行四边形的性质和判定得出平行四边形,求出D的坐标,把D的坐标代入抛物线的解析式,左边=右边,即得出D在抛物线上,即可得出答案;
(4)根据勾股定理,可得AP的长,根据线段的和差,可得PM的长,MN的长,根据相似三角形的判定与性质,可得关于b的方程,根据解方程,可得答案.
解答 解:(1)如图1,作CH⊥AB于H点.
∵CH=1,半径CB=2,
∴HB=$\sqrt{3}$,
∴A的坐标是(1-$\sqrt{3}$,0),B的坐标是(1+$\sqrt{3}$,0).
(2)设抛物线的解析式是y=a(x-1)2+3,
把点B(1+$\sqrt{3}$,0)代入上式,解得:a=-1,
∴y=-(x-1)2+3=-x2+2x+2,
即抛物线的解析式是y=-x2+2x+2.
(3)如图2:
假设存在点D使线段OP与CD互相平分,
则四边形OCPD是平行四边形,
∴PC∥OD,PC=OD,
∵PC∥y轴,
∴点D在y轴上,
∵PC=2,
∴OD=2,
即D(0,2),∠MPN=
又D(0,2)满足y=-x2+2x+2,
∴点D在抛物线上,
∴存在D点,使线段OP与CD互相平分,且点D的坐标是(0,2);
(4)如图3: ,
,
作MN⊥AP,
设M(1,b)PM=(1-b),MN=MH=b,
HA=1-(1-$\sqrt{3}$)=$\sqrt{3}$,
AP=$\sqrt{A{H}^{2}+P{H}^{2}}$=$\sqrt{(\sqrt{3})^{2}+{3}^{2}}$=2$\sqrt{3}$.
由∠MPN=∠APH,∠MNP=∠AHP=90°,得
△MNP∽△AHP,
$\frac{MN}{AH}$=$\frac{PM}{AP}$,即$\frac{b}{\sqrt{3}}$=$\frac{3-b}{2\sqrt{3}}$,
解得b=1,
即M(1,1).
点评 本题综合考查对平行四边形的性质和判定,平行线的性质,勾股定理,用待定系数法求二次函数的解析式,垂径定理等知识点,本题综合性较强,通过做题培养学生分析问题和解决问题的能力,题型较好,难度适中.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
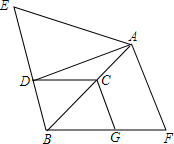 如图,已知点A在∠EBF的角平分线上,C为AB的中点,CD∥BF,CD交BE于点D,
如图,已知点A在∠EBF的角平分线上,C为AB的中点,CD∥BF,CD交BE于点D,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
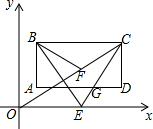 如图,在平面直角坐标系中,第一象限内长方形ABCD,AD∥x轴,点E在x轴上,EC交AD于G,BF平分∠CBE交OC于F,若∠CGD=2∠OCE,则下列结论正确的是( )
如图,在平面直角坐标系中,第一象限内长方形ABCD,AD∥x轴,点E在x轴上,EC交AD于G,BF平分∠CBE交OC于F,若∠CGD=2∠OCE,则下列结论正确的是( )| A. | ∠BEC=∠BFO | B. | ∠BEC+∠BFO=135° | C. | $\frac{1}{2}$∠BEC+∠BFO=90° | D. | ∠BEC+$\frac{1}{2}$∠BFO=90° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1.5 | B. | -7.5 | C. | 1.5 | D. | 7.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x+$\frac{1}{x}$=0 | B. | ax2+bx+c=0 | C. | (x-1)(x+2)=1 | D. | 3x2-2xy-5y2=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com