解:(1)(x-5)
2-9=0;
(x-5)
2=9,
∴x-5=±3,
∴x
1=8,x
2=2,
(2)3x
2-1=6x,
∴3x
2-6x-1=0,
△=b
2-4ac=36+12=48,
x=

=
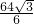
∴x
1=1+

,x
2=1-

,
(3)x
2+2x-63=0,
∴(x-7)(x+9)=0,
∴x
1=7,x
2=-9,
(4)
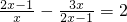
,
先设
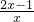
=y,根据题意得:
y-
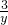
=2,
∴y
2-2y-3=0,
(y-3)(y+1)=0,
∴y-3=0或y+1=0,
∴y
1=3,y
2=-1,
∴
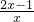
=3,或
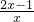
=-1,
∴x
1=-1,x
2=

;
把x
1=-1和x
2=

分别代入x-1中,都不等于0,
∴x
1=-1,x
2=

是原方程的解;
(5)

,
由①得:x=13-y,
∴(13-y-1)(y-1)=30,
∴(12-y)(y-1)=30,
∴y
2-13y+42=0,
(y-6)(y-7)=0,
∴y
1=6,y
2=7,
∴x
1=13-6=7,x
2=13-7=6,
∴

,

;
(6)
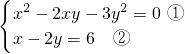
,
由②得:x=6+2y,
∴(6+2y)
2-2(6+2y)y-3y
2=0,
y
2-4y-12=0,
(y-6)(y+2)=0,
∴y
1=6,y
2=-2,
∴x
1=18,x
2=2,
∴
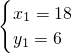
,

.
分析:(1)利用直接开平方法解方程即可得出答案;
(2)利用公式法求出△的符号,再利用公式求出即可;
(3)将等式左边因式分解,转化成两个一元一次方程,求解即可.
(4)先设
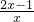
=y,再根据原式整理成y
2-2y-3=0,即可求出y的值,再把y的值代入先设
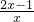
中即可求出x的值,再进行检验,即可求出答案.
(5)利用代入消元法,将x=13-y,代入方程②,求出y的值,进而得出x的值;
(6)利用代入消元法,将x=6+2y,代入方程①,求出y的值,进而得出x的值.
点评:此题主要考查了解一元二次方程以及分式方程和二元二次方程组,根据题目的结构特点选择适当的方法,进行降次解方程是本题的关键.

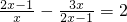

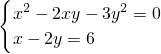 .
. =
=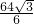
 ,x2=1-
,x2=1- ,
,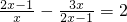 ,
,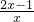 =y,根据题意得:
=y,根据题意得: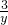 =2,
=2,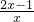 =3,或
=3,或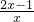 =-1,
=-1, ;
; 分别代入x-1中,都不等于0,
分别代入x-1中,都不等于0, 是原方程的解;
是原方程的解; ,
, ,
, ;
;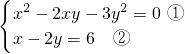 ,
,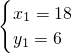 ,
, .
.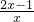 =y,再根据原式整理成y2-2y-3=0,即可求出y的值,再把y的值代入先设
=y,再根据原式整理成y2-2y-3=0,即可求出y的值,再把y的值代入先设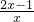 中即可求出x的值,再进行检验,即可求出答案.
中即可求出x的值,再进行检验,即可求出答案.
