

分析 (1)根据题意列式计算出部分的人数,最后补全统计图即可;
(2)根据题意列式计算即可;
(3)根据题意列式计算即可.
解答 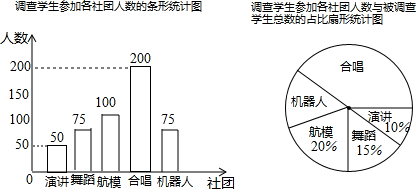 解:(1)参加本次调查的学生有:50÷10%=500名;
解:(1)参加本次调查的学生有:50÷10%=500名;
参加舞蹈的有:500×15%=75名,
参加航模的有:500×20%=100名,
参加机器人的有:500-75-100-50-200=75名;
如图所示;
(2)360°×$\frac{75}{500}$=54°,
∴在扇形图中,表示机器人扇形的圆心角的度数为54度;
(3)3000×$\frac{200}{500}$=1200名,
答:校共有1200名学生参加了合唱社团.
故答案为:500,54,1200.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
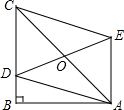 如图,在Rt△ABC中,∠B=90°,AB=10,BC>AB,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是10.
如图,在Rt△ABC中,∠B=90°,AB=10,BC>AB,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是10.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
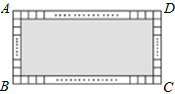 如图所示的是由一个小矩形与52个边长为1的小正方形组成的大矩形,小矩形的长与宽之比是7:5,若设小矩形的长为x,宽为y,则根据题意可列方程组( )
如图所示的是由一个小矩形与52个边长为1的小正方形组成的大矩形,小矩形的长与宽之比是7:5,若设小矩形的长为x,宽为y,则根据题意可列方程组( )| A. | $\left\{\begin{array}{l}{x:y=7:5}\\{2(x+y)+4=52}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x:y=5:7}\\{2(x+y)+4=52}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x:y=5:7}\\{x+y=52}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x:y=7:5}\\{2(x+y)=52}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
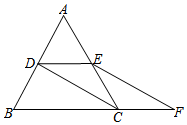 如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连结CD和EF.
如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连结CD和EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
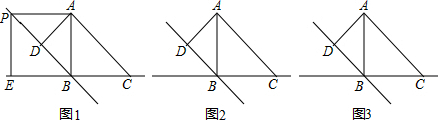
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com