
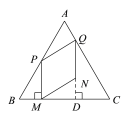
ЁОЬтФПЁПШчЭМЃЌдкЕШБпЁїABCжаЃЌ ![]() ЃЎЖЏЕуPДгЕуBГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуAдЫЖЏЃЛЭЌЪБЖЏЕуQДгЕуAГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуCдЫЖЏЃЎзїPMЁЭBCгкЕуMЃЌСЌНсPQЃЎвдPMЁЂPQЮЊСкБпзїЁѕPMNQЃЌЩшЁѕPMNQгыЁїABCжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊSЃЌЕуQЕФдЫЖЏЪБМфЮЊtУыЃЎ
ЃЎЖЏЕуPДгЕуBГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуAдЫЖЏЃЛЭЌЪБЖЏЕуQДгЕуAГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуCдЫЖЏЃЎзїPMЁЭBCгкЕуMЃЌСЌНсPQЃЎвдPMЁЂPQЮЊСкБпзїЁѕPMNQЃЌЩшЁѕPMNQгыЁїABCжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊSЃЌЕуQЕФдЫЖЏЪБМфЮЊtУыЃЎ
ЃЈ1ЃЉ![]() _____________ЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉЃЎ
_____________ЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉЃЎ
ЃЈ2ЃЉЕБЫФБпаЮPMNQЪЧСтаЮЪБЃЌЧѓtЕФжЕЃЎ
ЃЈ3ЃЉЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ1ЃЛЃЈ3ЃЉ
ЃЛЃЈ2ЃЉ1ЃЛЃЈ3ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОн30ЖШЕФжБНЧШ§НЧаЮЕФаджЪПЩЕУPMЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌзїИЈжњЯпЃЌЙЙНЈжБНЧШ§НЧаЮЃЌИљОнЙДЙЩЖЈРэКЭ30ЁуЕФжБНЧШ§НЧаЮЕФаджЪЕУЃКAGКЭPGЕФГЄЃЌИљОнAB=4ЃЌСаЗНГЬПЩЕУtЕФжЕЃЛ
ЃЈ3ЃЉЗжШ§жжЧщПіЃКЂй0ЁмtЃМ![]() ЪБЃЌШчЭМ3ЃЌбгГЄQNНЛBCгкGЃЌЁѕPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЁѕPMNQЃЛ
ЪБЃЌШчЭМ3ЃЌбгГЄQNНЛBCгкGЃЌЁѕPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЁѕPMNQЃЛ
ЂкЕБ![]() ЁмtЃМ2ЪБЃЌШчЭМ4ЃЌЁѕPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЬнаЮPMGQЃЛ
ЁмtЃМ2ЪБЃЌШчЭМ4ЃЌЁѕPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЬнаЮPMGQЃЛ
ЂлЕБ2ЁмtЁм4ЪБЃЌШчЭМ5ЃЌPгыAжиКЯЃЌЁѕPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЬнаЮPMGQЃЌИљОнУцЛ§ЙЋЪНПЩЕУНсТлЃЎ
НтЃКЃЈ1ЃЉЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯB=60ЁуЃЌ
ЁпPMЁЭBCЃЌ
ЁрЁЯPMB=90ЁуЃЌ
ЁпPB=2tЃЌ
ЁрPM=![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЫФБпаЮPMNQЪЧСтаЮЃЌ

Й§QзїQGЁЭABгкGЃЌ
гЩЬтвтЕУЃКAQ=tЃЌPB=2tЃЌ
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯA=ЁЯB=60ЁуЃЌ
ЁрЁЯAQG=30ЁуЃЌ
ЁрAG=![]() ЃЌGQ=
ЃЌGQ=![]() ЃЌ
ЃЌ
RtЁїBPMжаЃЌЁЯBMP=90ЁуЃЌ
ЁрЁЯBPM=30ЁуЃЌ
ЁрPM=![]() ЃЌ
ЃЌ
ЁпЫФБпаЮPMNQЪЧСтаЮЃЌ
ЁрPQ=PM=![]() ЃЌ
ЃЌ
ЁрPG=![]() ЃЌ
ЃЌ
ЁрAB=AG+PG+PBЃЌМД2t+![]() +
+![]() =4ЃЌ
=4ЃЌ
Ёрt=1ЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕБNдкBCЩЯЪБЃЌЫФБпаЮPMNQЪЧОиаЮЃЌ

ЁрPQЁЮBCЃЌ
ЁрЁЯAPQ=ЁЯB=60ЁуЃЌЁЯAQP=ЁЯC=60ЁуЃЌ
ЁрЁїAPQЪЧЕШБпШ§НЧаЮЃЌ
ЁрAP=AQ=tЃЌ
ЁрAB+PB=4ЃЌМДt+2t=4ЃЌ
Ёрt=![]() ЃЛ
ЃЛ
ЗжШ§жжЧщПіЃК
Ђй0ЁмtЃМ![]() ЪБЃЌШчЭМЃЌбгГЄQNНЛBCгкGЃЌPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЁѕPMNQЃЌ
ЪБЃЌШчЭМЃЌбгГЄQNНЛBCгкGЃЌPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЁѕPMNQЃЌ

ЁпPMЁЮQNЃЌPMЁЭBCЃЌ
ЁрQGЁЭBCЃЌ
RtЁїCQGжаЃЌЁЯCQG=30ЁуЃЌCQ=4-tЃЌ
ЁрGQ=![]() ЃЈ4-tЃЉЃЌCG=
ЃЈ4-tЃЉЃЌCG=![]() CQ=
CQ=![]() ЃЈ4-tЃЉЃЌ
ЃЈ4-tЃЉЃЌ
ЁрMG=![]() ЃЌ
ЃЌ
ЁрS=SPMNQ=PMMG=![]() ЃЛ
ЃЛ
ЂкЕБ![]() ЁмtЃМ2ЪБЃЌШчЭМЃЌPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЬнаЮPMGQЃЌ
ЁмtЃМ2ЪБЃЌШчЭМЃЌPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЬнаЮPMGQЃЌ

ЁрS=![]() MG(QG+PM)=
MG(QG+PM)=![]() ЃЛ
ЃЛ
ЂлЕБ2ЁмtЁм4ЪБЃЌШчЭМЃЌPгыAжиКЯЃЌPMNQгыЁїABCжиЕўВПЗжЭМаЮЪЧЬнаЮPMGQЃЌ

BM=2ЃЌPM=![]() ЃЌCG=
ЃЌCG=![]() ЃЌ
ЃЌ
ЁрMG=![]() =
=![]() ЃЌ
ЃЌ
ЁрS=![]() MG(QG+PM)=
MG(QG+PM)=![]() ЃЛ
ЃЛ
Ёр .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABC жаЃЌAB=ACЃЌAE ЪЧЁЯBAC ЕФЦНЗжЯпЃЌЁЯABC ЕФЦНЗжЯп BM НЛ AE гкЕу MЃЌЕу Oдк AB ЩЯЃЌвдЕуO ЮЊдВаФЃЌOB ЕФГЄЮЊАыОЖЕФдВОЙ§Еу MЃЌНЛ BC гкЕуGЃЌНЛ AB гкЕу FЃЎ
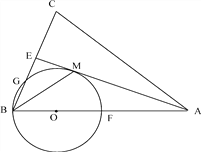
ЃЈ1ЃЉЧѓжЄЃКAE ЮЊЁбO ЕФЧаЯпЃЎ
ЃЈ2ЃЉЕБ BC=8ЃЌAC=12 ЪБЃЌЧѓЁбO ЕФАыОЖЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЧѓЯпЖЮ BG ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
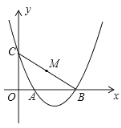
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() НЛxжсгкЕуAЃЌBЃЌНЛyжсгкЕуCЃЌЕБ
НЛxжсгкЕуAЃЌBЃЌНЛyжсгкЕуCЃЌЕБ![]() жНЦЌЩЯЕФCбизХДЫХзЮяЯпдЫЖЏЪБЃЌдђ
жНЦЌЩЯЕФCбизХДЫХзЮяЯпдЫЖЏЪБЃЌдђ![]() жНЦЌЫцжЎвВИњзХЫЎЦНвЦЖЏЃЌЩшжНЦЌЩЯCBЕФжаЕуMзјБъЮЊ
жНЦЌЫцжЎвВИњзХЫЎЦНвЦЖЏЃЌЩшжНЦЌЩЯCBЕФжаЕуMзјБъЮЊ![]() ЃЌдкДЫдЫЖЏЙ§ГЬжаЃЌnгыmЕФЙиЯЕЪНЪЧЃЈ ЃЉ
ЃЌдкДЫдЫЖЏЙ§ГЬжаЃЌnгыmЕФЙиЯЕЪНЪЧЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊaЁЂbЁЂcЮЊе§Ъ§ЃЌШєЙигкxЕФвЛдЊЖўДЮЗНГЬax2+bx+cЃН0гаСНИіЪЕЪ§ИљЃЌдђЙигкxЕФЗНГЬa2x2+b2x+c2ЃН0НтЕФЧщПіЮЊ(ЁЁЁЁ)
A.гаСНИіВЛЯрЕШЕФе§ИљB.гавЛИіе§ИљЃЌвЛИіИКИљ
C.гаСНИіВЛЯрЕШЕФИКИљD.ВЛвЛЖЈгаЪЕЪ§Иљ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
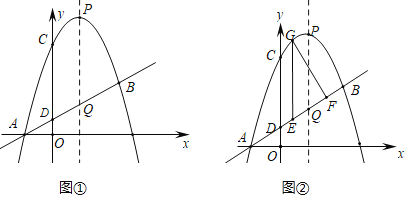
ЁОЬтФПЁПШчЭМЂйХзЮяЯпyЃНЉx2+ЃЈmЉ1ЃЉx+mгыжБЯпyЃНkx+kНЛгкЕуAЁЂBЃЌЦфжаAЕудкxжсЩЯЃЌЫќУЧгыyжсНЛЕуЗжБ№ЮЊCКЭDЃЌPЮЊХзЮяЯпЕФЖЅЕуЃЌЧвЕуPзнзјБъЮЊ4ЃЌХзЮяЯпЕФЖдГЦжсНЛжБЯпгкЕуQЃЎ
ЃЈ1ЃЉЪдгУКЌkЕФДњЪ§ЪНБэЪОЕуQЁЂЕуBЕФзјБъЃЎ
ЃЈ2ЃЉСЌНгPCЃЌШєЫФБпаЮCDQPЕФФкВПЃЈАќРЈБпНчКЭЖЅЕуЃЉжЛга4ИіКсзјБъЁЂзнзјБъОљЮЊећЪ§ЕФЕуЃЌЧѓkЕФШЁжЕЗЖЮЇЃЎ
ЃЈ3ЃЉШчЭМЂкЃЌЫФБпаЮCDQPЮЊЦНааЫФБпаЮЪБЃЌ
ЂйЧѓkЕФжЕЃЛ
ЂкEЁЂFЮЊЯпЖЮDBЩЯЕФЕуЃЈКЌЖЫЕуЃЉЃЌКсзјБъЗжБ№ЮЊaЃЌa+nЃЈnЮЊе§ећЪ§ЃЉЃЌEGЁЮyжсНЛХзЮяЯпгкЕуGЃЎЮЪЪЧЗёДцдке§ећЪ§nЃЌЪЙТњзуtanЁЯEGF![]() ЕФЕуEгаСНИіЃПШєДцдкЃЌЧѓГіnЃЛШєВЛДцдкЫЕУїРэгЩЃЎ
ЕФЕуEгаСНИіЃПШєДцдкЃЌЧѓГіnЃЛШєВЛДцдкЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкxЕФвЛдЊЖўДЮЗНГЬx2+ЃЈ2k+1ЃЉx+k2+1=0гаСНИіВЛЕШЪЕИљx1ЁЂx2ЃЎ
ЃЈ1ЃЉЧѓЪЕЪ§kЕФШЁжЕЗЖЮЇЃЎ
ЃЈ2ЃЉШєЗНГЬСНЪЕИљx1ЁЂx2Тњзуx1+x2=Љx1x2ЃЌЧѓkЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдРЌЛјНјааЗжРрЭЖЗХЃЌФмЬсИпРЌЛјДІРэКЭдйРћгУЕФаЇТЪЃЌМѕЩйЮлШОЃЌБЃЛЄЛЗОГЃЎЮЊСЫМьВщРЌЛјЗжРрЕФТфЪЕЧщПіЃЌФГОгЮЏЛсГЩСЂСЫМзЁЂввСНИіМьВщзщЃЌВЩШЁЫцЛњГщВщЕФЗНЪНЗжБ№ЖдЯНЧјФкЕФ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЫФИіаЁЧјНјааМьЫЃЌВЂЧвУПИіаЁЧјВЛжиИДМьВщЃЎ
ЫФИіаЁЧјНјааМьЫЃЌВЂЧвУПИіаЁЧјВЛжиИДМьВщЃЎ
ЃЈ1ЃЉМззщГщЕН![]() аЁЧјЕФИХТЪЪЧ___________ЃЛ
аЁЧјЕФИХТЪЪЧ___________ЃЛ
ЃЈ2ЃЉЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓМззщГщЕН![]() аЁЧјЃЌЭЌЪБввзщГщЕН
аЁЧјЃЌЭЌЪБввзщГщЕН![]() аЁЧјЕФИХТЪЃЎ
аЁЧјЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТУцВФСЯЃК
аЁКьгіЕНетбљвЛИіЮЪЬтЃКШчЭМ1ЃЌдкЫФБпаЮABCDжаЃЌЁЯA=ЁЯC=90ЁуЃЌЁЯD=60ЁуЃЌAB=![]() ЃЌBC=
ЃЌBC=![]() ЃЌЧѓADЕФГЄЃЎ
ЃЌЧѓADЕФГЄЃЎ
аЁКьЗЂЯжЃЌбгГЄABгыDCЯрНЛгкЕуEЃЌЭЈЙ§ЙЙдьRtЁїADEЃЌОЙ§ЭЦРэКЭМЦЫуФмЙЛЪЙЮЪЬтЕУЕННтОі(ШчЭМ2)ЃЎ
ЧыЛиД№ЃКADЕФГЄЮЊЁЁЁЁЁЁЁЁЃЎ
ВЮПМаЁКьЫМПМЮЪЬтЕФЗНЗЈЃЌНтОіЮЪЬтЃК
ШчЭМ3ЃЌдкЫФБпаЮABCDжаЃЌtanA=![]() ЃЌЁЯB=ЁЯC=135ЁуЃЌAB=9ЃЌCD=3ЃЌЧѓBCКЭADЕФГЄЃЎ
ЃЌЁЯB=ЁЯC=135ЁуЃЌAB=9ЃЌCD=3ЃЌЧѓBCКЭADЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§![]() (aЃЌbЃЌcЮЊГЃЪ§ЃЌЧвaЁй0)жаЕФxгыyЕФВПЗжЖдгІжЕШчЯТБэЃК
(aЃЌbЃЌcЮЊГЃЪ§ЃЌЧвaЁй0)жаЕФxгыyЕФВПЗжЖдгІжЕШчЯТБэЃК
x | Ё | -1 | 0 | 1 | 3 | Ё |
y | Ё | -3 | 1 | 3 | 1 | Ё |
дђЯТСаХаЖЯжае§ШЗЕФЪЧЃЈ ЃЉ
A.ХзЮяЯпПЊПкЯђЩЯB.ХзЮяЯпгыyжсНЛгкИКАыжс
C.ХзЮяЯпЕФЖЅЕуЮЊ(1ЃЌ3)D.вЛдЊЖўДЮЗНГЬax2+bx+c=0ЕФе§Иљдк3гы4жЎМф
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com