
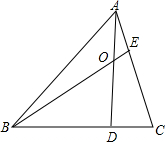
 如图,已知在△ABC中,BD:DC=3:1,AE:CE=1:2,S△ABC=48,求四边形ODCE的面积.
如图,已知在△ABC中,BD:DC=3:1,AE:CE=1:2,S△ABC=48,求四边形ODCE的面积. 分析 连接CO,设S△COE=x,S△COD=y,根据BD:DC=3:1,AE:CE=1:2,确定三角形面积之间的等量关系,求出x和y之间的关系式,然后根据△ABC的面积解得x,最后求出四边形ODCE的面积.
解答 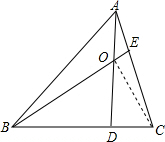 解:连接CO,设S△COE=x,S△COD=y,
解:连接CO,设S△COE=x,S△COD=y,
∵AE:CE=1:2,
∴$\frac{{S}_{△COE}}{{S}_{△AOE}}$=$\frac{{S}_{△BCE}}{{S}_{△ABE}}$=$\frac{CE}{AE}$=2,
∴S△AOE=$\frac{1}{2}$x,
∵BD:DC=3:1,
∴$\frac{{S}_{△OCD}}{{S}_{△OBD}}$=$\frac{{S}_{△ADC}}{{S}_{△ADB}}$=$\frac{1}{3}$,
∴S△OBD=3y,
∵3(x+$\frac{1}{2}$x+y)-3y=$\frac{1}{2}$(x+y+3y)-$\frac{1}{2}$x
∴$\frac{9}{2}$x=2y,即y=$\frac{9}{4}$x,
∵△ABC的面积S△ABC=48,
∴4(x+$\frac{1}{2}$x+y)=48,
∴x+$\frac{1}{2}$x+$\frac{9}{4}$x=12
解得x=$\frac{16}{5}$,
故四边形ODCE的面积=x+y=$\frac{16}{5}$+$\frac{9}{4}$×$\frac{16}{5}$=$\frac{52}{5}$.
点评 本题主要考查三角形的面积的知识点,根据等高的三角形的面积与底边成比例进行解答,此题需要同学们熟练掌握.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:选择题
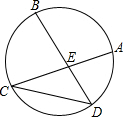 如图,弦AC、BD相交于点E,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,若∠AED=80°,则∠ACD的度数为( )
如图,弦AC、BD相交于点E,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,若∠AED=80°,则∠ACD的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 15° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
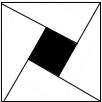 由四个全等的直角三角形拼成如图所示的“赵爽弦图”,若直角三角形斜边长为2,最短的之边长为1,则图中阴影部分的面积为( )
由四个全等的直角三角形拼成如图所示的“赵爽弦图”,若直角三角形斜边长为2,最短的之边长为1,则图中阴影部分的面积为( )| A. | 1 | B. | 3 | C. | 4-2$\sqrt{3}$ | D. | 4+2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
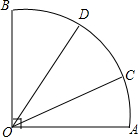 如图,∠AOB=90°,OA=OB,C、D是$\widehat{AB}$上的两点,∠AOD>∠AOC.
如图,∠AOB=90°,OA=OB,C、D是$\widehat{AB}$上的两点,∠AOD>∠AOC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com