
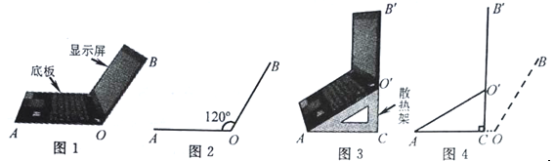
【题目】小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架ACO'后,电脑转到AO'B'位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O'C⊥OA于点C,O'C=12cm.
(1)求∠CAO'的度数.
(2)显示屏的顶部B'比原来升高了多少?
(3)如图4,垫入散热架后,要使显示屏O'B'与水平线的夹角仍保持120°,则显示屏O'B'应绕点O'按顺时针方向旋转多少度?
【答案】(1)∠CAO′=30°;(2)(36﹣12![]() )cm;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°.
)cm;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°.
【解析】试题分析:(1)通过解直角三角形即可得到结果;
(2)过点B作BD⊥AO交AO的延长线于D,通过解直角三角形求得BD=OBsin∠BOD=24×![]() =12
=12![]() ,由C、O′、B′三点共线可得结果;
,由C、O′、B′三点共线可得结果;
(3)显示屏O′B′应绕点O′按顺时针方向旋转30°,求得∠EO′B′=∠FO′A=30°,既是显示屏O′B′应绕点O′按顺时针方向旋转30°.
试题解析:(1)∵O′C⊥OA于C,OA=OB=24cm,
∴sin∠CAO′=![]() ,
,
∴∠CAO′=30°;
(2)过点B作BD⊥AO交AO的延长线于D,∵sin∠BOD=![]() ,∴BD=OBsin∠BOD,∵∠AOB=120°,∴∠BOD=60°,∴BD=OBsin∠BOD=24×
,∴BD=OBsin∠BOD,∵∠AOB=120°,∴∠BOD=60°,∴BD=OBsin∠BOD=24×![]() =12
=12![]() ,∵O′C⊥OA,∠CAO′=30°,
,∵O′C⊥OA,∠CAO′=30°,
∴∠AO′C=60°,∵∠AO′B′=120°,∴∠AO′B′+∠AO′C=180°,
∴O′B′+O′C﹣BD=24+12﹣12![]() =36﹣12
=36﹣12![]() ,
,
∴显示屏的顶部B′比原来升高了(36﹣12![]() )cm;
)cm;
(3)显示屏O′B′应绕点O′按顺时针方向旋转30°,
理由:∵显示屏O′B与水平线的夹角仍保持120°,
∴∠EO′F=120°,
∴∠FO′A=∠CAO′=30°,
∵∠AO′B′=120°,
∴∠EO′B′=∠FO′A=30°,
∴显示屏O′B′应绕点O′按顺时针方向旋转30°.


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点A(a、b)是一次函数y=x+m的图像与反比例函数![]() 的图像在第一象限的交点,且S△ABO=3。
的图像在第一象限的交点,且S△ABO=3。

①根据这些条件你能够求出反比例函数的解析式吗?如果能够,请你求出来,如果不能,请说明理由。
②你能够求出一次函数的函数关系式吗?如果能,请你求出来,如果不能,请你说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
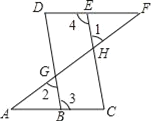
【题目】如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由.
解:∵∠1=∠2(已知)
∠2=∠DGF
∴∠1=∠DGF(____________)
∴BD∥CE
∴∠3+∠C=180°( )
又∵∠3=∠4(已知)
∴∠4+∠C=180°
∴ ∥ (同旁内角互补,两直线平行)
∴∠A=∠F( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN.

查看答案和解析>>
科目:初中数学 来源: 题型:
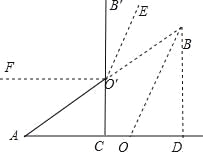
【题目】如图,平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.
(1)求AB的长度;
(2)以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.求证:BD=OE;
(3)在(2)的条件下,连接DE交AB于F.求证:F为DE的中点.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程组![]() 的解x、y满足:x为非正数,y为负数.
的解x、y满足:x为非正数,y为负数.
(1)求a的取值范围;
(2)在a的取值范围中,当a为何整数时,关于x的不等式2ax+x>2a+1的解集为x<1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,他手中持有的钱数(含备用零钱)y与售出的土豆千克数x的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是______元,降价前他每千克土豆出售的价格是______元;
(2)降价后他按每千克0.8元将剩余土豆售完,这时他手中的钱(含备用零钱)是62元,求降价后的线段所表示的函数表达式并写出它的取值范围.
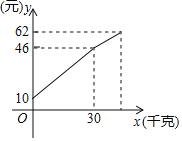
查看答案和解析>>
科目:初中数学 来源: 题型:
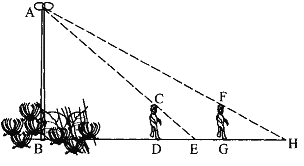
【题目】如图,花丛中有一路灯杆AB. 在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米. 如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
查看答案和解析>>
科目:初中数学 来源: 题型:
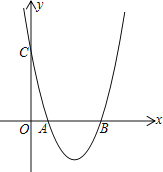
【题目】如图1,抛物线y=x2+bx+c与x轴交于A(1,0)、B(4,0),与y轴交于点C
(1) 求抛物线的解析式
(2) 抛物线上一点D,满足S△DAC=S△OAC,求点D的坐标
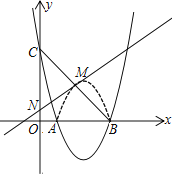
(3) 如图2,已知N(0,1),将抛物线在点A、B之间部分(含点A、B)沿x轴向上翻折,得到图T(虚线部分),点M为图象T的顶点.现将图象保持其顶点在直线MN上平移,得到的图象T1与线段BC至少有一个交点,求图象T1的顶点横坐标的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com