
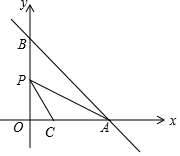
 如图,在平面直角坐标系xOy中,直线y=-x+m分别交x轴,y轴于A,B两点,已知点C(2,0).
如图,在平面直角坐标系xOy中,直线y=-x+m分别交x轴,y轴于A,B两点,已知点C(2,0).分析 (1)把点C的坐标代入函数解析式求得m的值;然后结合一次函数解析式求得A、B的坐标,然后利用等积法求得点O到直线AB的距离是 $\sqrt{2}$;
(2)典型的“一线三等角”,构造相似三角形△PCD∽△APB,对m的取值分析进行讨论,在m<0时,点A在x轴的负半轴,而此时,∠APC>∠OBA=45°,不合题意;故m>0.由相似比求得边的相应关系.
解答  解:(1)当直线AB经过点C时,点A与点C重合,
解:(1)当直线AB经过点C时,点A与点C重合,
当x=2时,y=-2+m=0,即m=2,
所以直线AB的解析式为y=-x+2,则B(0,2).
∴OB=OA=2,AB=2$\sqrt{2}$.
设点O到直线AB的距离为d,
由S△OAB=$\frac{1}{2}$OA2=$\frac{1}{2}$AB•d,得
4=2$\sqrt{2}$d,
则d=$\sqrt{2}$.
故答案是:$\sqrt{2}$.
(2)作OD=OC=2,连接CD.则∠PDC=45°,如图,
由y=-x+m可得A(m,0),B(0,m).
所以OA=OB,
则∠OBA=∠OAB=45°.
当m<0时,∠APC>∠OBA=45°,
所以,此时∠CPA>45°,故不合题意.
所以m>0.
因为∠CPA=∠ABO=45°,
所以∠BPA+∠OPC=∠BAP+∠BPA=135°,即∠OPC=∠BAP,则△PCD∽△APB,
所以$\frac{PD}{AB}$=$\frac{CD}{PB}$,即$\frac{\frac{1}{2}m+2}{\sqrt{2}m}$=$\frac{2\sqrt{2}}{\frac{1}{2}m}$,
解得m=12.
故答案是:12.
点评 本题考查了一次函数综合题.需要掌握待定系数法求一次函数解析式,相似三角形的判定与性质,三角形面积的求法等知识点,另外,解题时,注意分类讨论数学思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
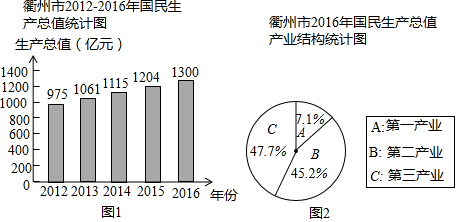
 某校举办一项小制作评比,作品上交时限为5月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的频数是12.请你回答:
某校举办一项小制作评比,作品上交时限为5月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的频数是12.请你回答:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
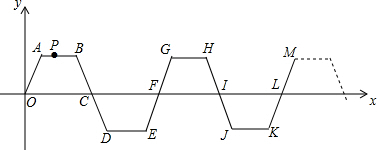
| A. | (1342,0) | B. | (1343,0) | C. | (1344,0) | D. | (1345,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com