
【题目】如图,![]() ,矩形
,矩形![]() 的边
的边![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() ,
,![]() ,矩形
,矩形![]() 沿射线
沿射线![]() 方向,以每秒1个单位长度的速度运动.同时点
方向,以每秒1个单位长度的速度运动.同时点![]() 从点
从点![]() 出发沿折线
出发沿折线![]() 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点![]() 运动,当点
运动,当点![]() 到达点
到达点![]() 时,矩形
时,矩形![]() 也停止运动,设点
也停止运动,设点![]() 的运动时间为
的运动时间为![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)分别写出点![]() 到
到![]() 、
、![]() 的距离(用含
的距离(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 不与矩形
不与矩形![]() 的顶点重合时,求
的顶点重合时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)设点![]() 到
到![]() 的距离为
的距离为![]() ,当
,当![]() 时,求
时,求![]() 的值;
的值;
(4)若在点![]() 出发的同时,点
出发的同时,点![]() 从点
从点![]() 以每秒
以每秒![]() 个单位长度的速度向终点A运动,当点
个单位长度的速度向终点A运动,当点![]() 停止运动时,点
停止运动时,点![]() 与矩形
与矩形![]() 也停止运动,设点
也停止运动,设点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,当
,当![]() 的一边与
的一边与![]() 的一边平行时,直接写出线段
的一边平行时,直接写出线段![]() 的长.
的长.
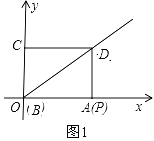
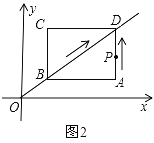
【答案】(1)![]() ,
,![]() ;(2)当0<t<3时,
;(2)当0<t<3时,![]() ;当3<t<7时,
;当3<t<7时,![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ,
,![]() ,
,![]()
【解析】
(1)过点B作x轴垂线,利用相似三角形可求得;
(2)分2种情况,一种是点P在AD上,另一种是点P在CD上,然后利用三角形面积公式可求得;
(3)直接令![]() 即可求出;
即可求出;
(4)存在3种情况,第一种是:QP∥BD,第二种是EP∥CD或EQ∥CB,第三种是QE∥BD,分别按照几何性质分析求解.
(1)如下图,过点B作x轴垂线,垂足为点M
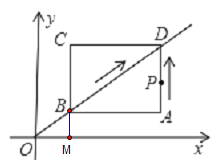
根据平移的特点,可得∠BOM=∠DBA
∵∠BMO=∠DAB=90°,∴△BMO∽△DAB
∵AB=4,AD=BC=3
∴BD=5
∵![]() ,OB=t
,OB=t
∴BM=![]() ,OM=
,OM=![]()
(2)情况一:当0<t<3时,图形如下,过点P作OD的垂线,交OD于点N
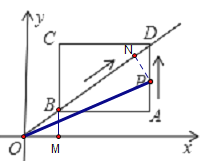
∵∠NDP=∠BDA,∠PND=∠BAD,∴△PND∽△BAD
∵AP=t,∴PD=3-t
∵![]() ,∴PN=
,∴PN=![]()
图中,OD=5+t
∴![]()
情况二:当3<t<7时,图形如下,过点P作OD的垂线,交OD于点N
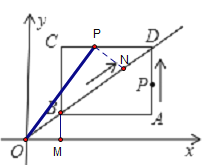
图中,PD=t-3,OD=5+t
同理,△PND∽△BCD,可得PN=![]()
∴![]()
(3)情况一:当0<t<3时
则h=PN=![]()
∵![]()
∴![]()
解得:t=![]()
情况二:当3<t<7时
则h=PN=![]()
∵![]()
∴![]()
解得:t=7(舍)
(4)情况一:QP∥BD,图形如下
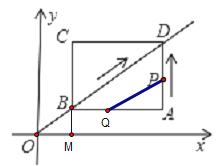
由题意可得:BQ=![]() ,AP=t,则QA=4-
,AP=t,则QA=4-![]() ,DP=3-t
,DP=3-t
∵BD∥QP
∴![]()
代入得:4![]()
解得:t=![]()
∴OD=5+t=![]()
情况二:如下图,EP∥CD(或EQ∥CB)
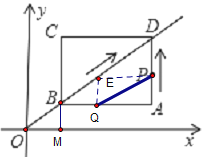
∵点E是点A关于QP对称的点
∴EP=PA,EQ=QA,QP=QP
∴△APQ≌△EPQ
∵EP∥CD,CD⊥AD
∴EP⊥AD
∴∠APQ=∠EPQ=45°
∴△AQP是等腰直角三角形,AQ=PA
∴4-![]()
解得:t=![]()
∴OD=5+t=![]()
情况三:如下图,QE∥BD,延长QE交DA于点N

∵△APQ≌△EPQ,∴∠QEP=∠QAP=90°
∴△ENP是等腰直角三角形
∵QN∥BD,∴∠NQA=∠DBA,∠A=∠A
∴△QNA∽△BDA
∵BQ=![]() ,AP=t,QA=4-
,AP=t,QA=4-![]() ,DP=3-t
,DP=3-t
∴![]()
∴QN=5-![]() ,NA=3-t
,NA=3-t
∴EN=QN-QE=QN-QA=1-![]() ,NP=NA-AP=3-2t,EP=PA=t
,NP=NA-AP=3-2t,EP=PA=t
∴在Rt△ENP中,![]()
解得:t=![]() 或t=3(舍)
或t=3(舍)
∴OD=5+t=![]()


科目:初中数学 来源: 题型:
【题目】今年 3 月 12 日植树节期间, 学校预购进 A、B 两种树苗,若购进 A种树苗 3 棵,B 种树苗 5 棵,需 2100 元,若购进 A 种树苗 4 棵,B 种树苗 10棵,需 3800 元.
(1)求购进 A、B 两种树苗的单价;
(2)若该单位准备用不多于 8000 元的钱购进这两种树苗共 30 棵,求 A 种树苗至少需购进多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题]小明在学习时遇到这样一个问题:求不等式x3+3x2﹣x﹣3>0的解集.
他经历了如下思考过程:
[回顾]
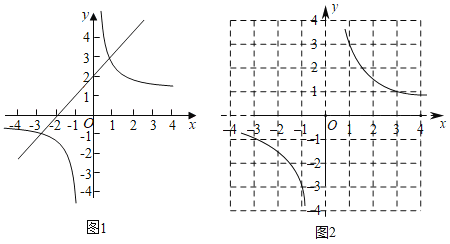
(1)如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=![]() 交于A (1,3)和B(﹣3,﹣1),则不等式ax+b>
交于A (1,3)和B(﹣3,﹣1),则不等式ax+b>![]() 的解集是 .
的解集是 .
[探究]将不等式x3+3x2﹣x﹣3>0按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,不等式两边同除以x并移项转化为x2+3x﹣1>![]() ;
;
当x<0时,不等式两边同除以x并移项转化为x2+3x﹣1<![]() .
.
(2)构造函数,画出图象:
设y3=x2+3x﹣1,y4=![]() ,在同一坐标系中分别画出这两个函数的图象;
,在同一坐标系中分别画出这两个函数的图象;
双曲线y4=![]() 如图2所示,请在此坐标系中画出抛物线y=x2+3x﹣1.(不用列表)
如图2所示,请在此坐标系中画出抛物线y=x2+3x﹣1.(不用列表)
(3)确定两个函数图象公共点的横坐标:
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 .
[解决]
(4)借助图象,写出解集:
结合“探究”中的讨论,观察两个函数的图象可知:不等式x3+3x2﹣x﹣3>0的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一批货物准备运往某地,有甲、乙、丙三辆卡车可雇用.已知甲、乙、丙三辆车每次运货量不变,且甲、乙两车单独运完这批货物分别用![]() 次;甲、丙两车合运相同次数,运完这批货物,甲车共运
次;甲、丙两车合运相同次数,运完这批货物,甲车共运![]() 吨;乙、丙两车合运相同次数,运完这批货物乙车共运
吨;乙、丙两车合运相同次数,运完这批货物乙车共运![]() 吨,现甲、乙、丙合运相同次数把这批货物运完,货主应付甲车主的运费为___________ 元.(按每吨运费
吨,现甲、乙、丙合运相同次数把这批货物运完,货主应付甲车主的运费为___________ 元.(按每吨运费![]() 元计算)
元计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
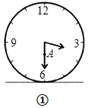
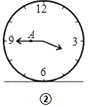
【题目】图①表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点![]() ,当钟面显示3点30分时,分针垂直于桌面,点
,当钟面显示3点30分时,分针垂直于桌面,点![]() 距离桌面的高度为
距离桌面的高度为![]() 公分,图②表示钟面显示3点45时,点
公分,图②表示钟面显示3点45时,点![]() 距桌面的高度为
距桌面的高度为![]() 公分,若钟面显示3点55时,点
公分,若钟面显示3点55时,点![]() 距离桌面的高度为__________公分.
距离桌面的高度为__________公分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达
两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达![]() 地后马上以另一速度原路返回
地后马上以另一速度原路返回![]() 地(掉头的时间忽略不计),乙车到达
地(掉头的时间忽略不计),乙车到达![]() 地以后即停在
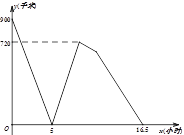
地以后即停在![]() 地等待甲车.如图所示为甲乙两车间的距离
地等待甲车.如图所示为甲乙两车间的距离![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (小时)之间的函数图象,则当乙车到达
(小时)之间的函数图象,则当乙车到达![]() 地的时候,甲车与
地的时候,甲车与![]() 地的距离为__________千米.
地的距离为__________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
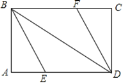
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:△AEB≌△CFD;
(2)当∠ABE= 度时,四边形BEDF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
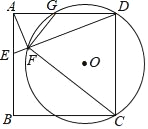
【题目】如图,在正方形ABCD中,E是AB上一点,连接DE.过点A作AF⊥DE,垂足为F,⊙O经过点C、D、F,与AD相交于点G.
(1)求证:△AFG∽△DFC;
(2)若正方形ABCD的边长为4,AE=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
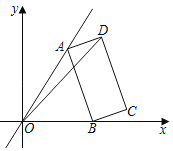
【题目】如图,在平面直角坐标系中,点A在一次函数y=![]() x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2
x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2![]() ,AD=1,则OD的最大值是( )
,AD=1,则OD的最大值是( )
A.![]() B.
B.![]() +2C.
+2C.![]() +2D.
+2D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com