
如图,在平面直角坐标系中,已知点A(0,12),B(16,0),动点P从点A开始在线段AO上以每秒1个单位的速度向点O移动,同时点Q从点B开始在BA上以每秒2个单位的速度向点A移动,设点P、Q移动的时间为t秒。
⑴求直线AB的解析式;
⑵求t为何值时,△APQ与△AOB相似?
⑶当t为何值时,△APQ的面积为 个平方单位?
个平方单位?
⑷当t为何值时,△APQ的面积最大,最大值是多少?
(1)y=-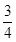 x+12;(2)
x+12;(2)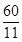 ,
,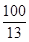 ;(3)2,8;(4)5,20.
;(3)2,8;(4)5,20.
解析试题分析:(1)设直线AB的解析式为y=kx+b,解得k,b即可;
(2)由AO=6,BO=8得AB=10,①当∠APQ=∠AOB时,△APQ∽△AOB利用其对应边成比例解t.②当∠AQP=∠AOB时,△AQP∽△AOB利用其对应边成比例解得t.
(3)根据△APQ的面积为 ,求出t的值.
,求出t的值.
(3)过点O作QE⊥AO于点E,利用t表示出△APQ的面积,利用函数的性质即可求解.
试题解析:(1)设直线AB的解析式为y=kx+b,
由题意,得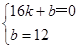
解得: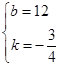
所以,直线AB的解析式为y=-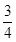 x+12;
x+12;
(2)由AO=12,BO=16得AB=20,
所以AP=t,AQ=20-2t,
①当∠APQ=∠AOB时,△APQ∽△AOB.
所以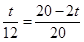 ,
,
解得t=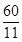 (秒),
(秒),
②当∠AQP=∠AOB时,△AQP∽△AOB.
所以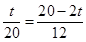 ,
,
解得t=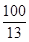 (秒);
(秒);
∴当t为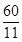 秒或
秒或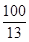 秒时,△APQ与△AOB相似;
秒时,△APQ与△AOB相似;
(3)过Q点作QE⊥Y轴于点E,
由△AQE∽△AOB知: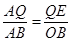
即: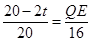
解得:QE=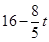
又S△APQ=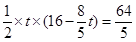
解得: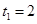 ,
,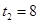
(4)∵QE=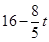
∴S△APQ= AP•QE=
AP•QE= t(
t(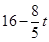 )=-
)=-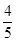 t2+8t=-
t2+8t=-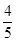 (t-5)2+20
(t-5)2+20
∴当t=5时,△APQ的面积最大,最大面积是20个平方单位.
考点: 一次函数综合题.


科目:初中数学 来源: 题型:解答题
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.
(1)这辆汽车的往、返速度是否相同?请说明理由;
(2)写出返程中y与x之间的函数表达式;并指出其中自变量的取值范围.
(3)求这辆汽车从甲地出发4h时与甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,一次函数y1=kx+b的图象与反比例函数y2=的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).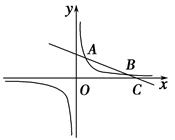
(1)求这两个函数的解析式;
(2)当x取何值时,y1>y2.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
函数常用的表示方法有三种.
已知A、B两地相距30千米,小王以40千米/时的速度骑摩托车从A地出发匀速前往B地参加活动.请选择两种方法来表示小王与B地的距离y(千米)与行驶时间x(小时)之间的函数关系.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知反比例函数y= (k为常数,k≠1)
(k为常数,k≠1)
(1)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(2)若在其图象的每一支上,y随x的增大而减小,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图:一次函数的图象与反比例函数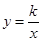 的图象交于A(-2,6)和点B(4,n)
的图象交于A(-2,6)和点B(4,n)
(1)求反比例函数的解析式和B点坐标
(2)根据图象回答,在什么范围时,一次函数的值大于反比例函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知 与
与 是反比例函数
是反比例函数 图象上的两个点.
图象上的两个点.
(1)求m和k的值
(2)若点C(-1,0),连结AC,BC,求△ABC的面积
(3)根据图象直接写出一次函数的值大于反比例函数的值的 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线y=kx-2与x轴、y轴分别交于B、C两点,OB:OC= .
.
(1)求B点的坐标和k的值.
(2)若点A(x,y)是第一象限内的直线y=kx-2上的一个动点,当点A运动过程中,①试写出△AOB的面积S与x的函数关系式;②探索:当点A运动到什么位置时,△AOB的面积是1.③在②成立的情况下,x轴上是否存在一点P,使△POA是等腰三角形.若存在,请写出满足条件的所有P点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com