
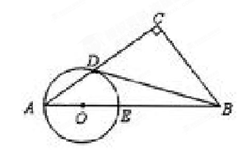
 ,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
 ,求⊙O的直径BC.
,求⊙O的直径BC.  ∴∠ODB+∠EDB=90
∴∠ODB+∠EDB=90
 =CF·CD
=CF·CD
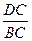 =
= 即
即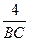 =
= 得直径BC=" 5 " ………………………………………10分
得直径BC=" 5 " ………………………………………10分 

科目:初中数学 来源: 题型:
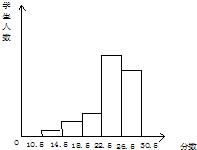 3、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.
3、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
(10分)如图,CD⊥AB于点D,BE⊥AC于点E,BE,CD交于点O,且AO平分∠BAC。
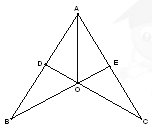
(1)求证:△ADO≌△AEO
(2)猜想OB与OC的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2010-2011学年山东省济南市学业水平模拟考试数学 题型:解答题
(本小题满分10分)
如图(1)所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图(2)所示.
已知展开图中每个正方形的边长为1.
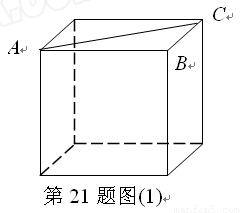
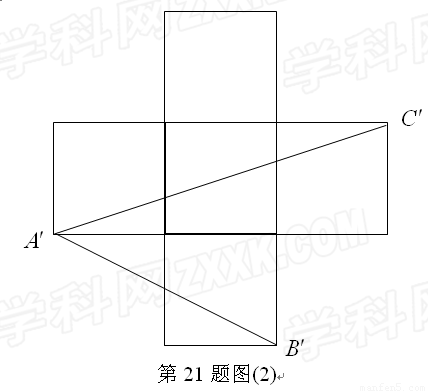
(1)求在该展开图中可画出最长线段的长度?这样的线段可画几条?
(2)试比较立体图中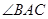 与平面展开图中
与平面展开图中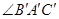 的大小关系?
的大小关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com