
【题目】如图,∠BCD=90°,BC=DC,直线PQ经过点D.设∠PDC=α(45°<α<135°),BA⊥PQ于点A,将射线CA绕点C按逆时针方向旋转90°,与直线PQ交于点E.
(1)判断:∠ABC ∠PDC(填“>”或“=”或“<”);
(2)猜想△ACE的形状,并说明理由;
(3)若△ABC的外心在其内部(不含边界),直接写出α的取值范围.
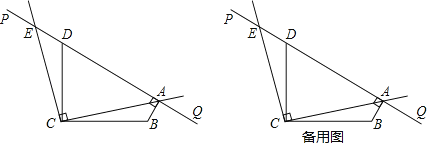
【答案】(1)=;(2)△ACE是等腰直角三角形,理由见解析;(3)45°<α<90°
【解析】
(1)利用四边形内角和等于360度得:∠B+∠ADC=180°,而∠ADC+∠EDC=180°,即可求解;
(2)证明△ABC≌△EDC(AAS)即可推知△ACE是等腰直角三角形;
(3)当∠ABC=α=90°时,△ABC的外心在其直角边上,∠ABC=α>90°时,△ABC的外心在其外部,即可求解.
解:(1)在四边形BADC中,∠B+∠ADC=360°﹣∠BAD﹣∠DCB=180°,
而∠ADC+∠EDC=180°,
∴∠ABC=∠PDC.
故答案是:=;
(2)△ACE是等腰直角三角形,理由如下:
∵∠ECD+∠DCA=90°,∠DCA+∠ACB=90°,
∴∠ACB=∠ECD.
由(1)知:∠ABC=∠PDC,
又∵BC=DC,
∴△ABC≌△EDC(AAS),
∴AC=CE.
又∵∠ACE=90°,
∴△ACE是等腰直角三角形;
(3)当∠ABC=α=90°时,△ABC的外心在其直角边上,
∠ABC=α>90°时,△ABC的外心在其外部,
而45°<α<135°,
故:45°<α<90°.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]()
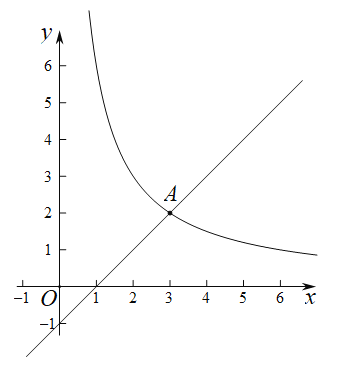
(1)求k的值;
(2)已知点![]() ,过点P作垂直于x轴的直线,交直线
,过点P作垂直于x轴的直线,交直线![]() 于点B,交函数
于点B,交函数![]() 于点C.
于点C.
①当![]() 时,判断线段
时,判断线段![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
②若![]() ,结合图象,直接写出n的取值范围.
,结合图象,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
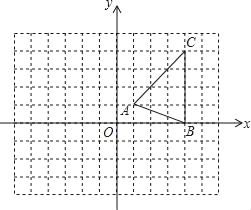
【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4).
(1)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2.
(2)求点C1在旋转过程中所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
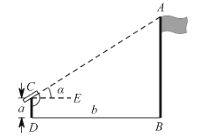
【题目】如图,小明想要测量学校操场上旗杆![]() 的高度,他作了如下操作:(1)在点
的高度,他作了如下操作:(1)在点![]() 处放置测角仪,测得旗杆顶的仰角
处放置测角仪,测得旗杆顶的仰角![]() ;(2)量得测角仪的高度
;(2)量得测角仪的高度![]() ;(3)量得测角仪到旗杆的水平距离
;(3)量得测角仪到旗杆的水平距离![]() .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
.利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习“三角形的内角和外角”时,老师在学案上设计了以下内容:
如图,已知△ABC,对∠A+∠B+∠ACB=180°的说理过程如下:
延长BC到点D,过点C作CE∥AB.
∵CE∥AB.
∴∠A=①(两直线平行,内错角相等).
∠B=②(两直线平行,同位角相等).
∵∠ACB+③+④=180°(平角定义).
∴∠A+∠B+∠ACB=180°(等量代换).
下列选项正确的是( )
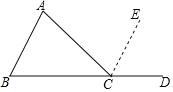
A.①处填∠ECDB.②处填∠ECDC.③处填∠AD.④处填∠B
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,AB=BC,点M从点D出发,沿D→C→A以1cm/s的速度匀速运动到点A,图2是点M运动时,△MAB的面积y(cm2)随时间x(s)变化的关系图象,则边AB的长为( )cm.
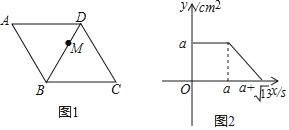
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
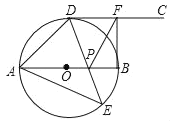
【题目】如图,AB为⊙O的直径,点D、E位于AB两侧的半圆上,射线DC切⊙O于点D,已知点E是半圆弧AB上的动点,点F是射线DC上的动点,连接DE、AE,DE与AB交于点P,再连接FP、FB,且∠AED=45°.
(1)求证:CD![]() AB;
AB;
(2)填空:
①当∠DAE= 时,四边形ADFP是菱形;
②当∠DAE= 时,四边形BFDP是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() (
(![]() )与双曲线
)与双曲线![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() 在第一象限),直线
在第一象限),直线![]() (
(![]() )与双曲线
)与双曲线![]() 交于
交于![]() ,
,![]() 两点.当这两条直线互相垂直,且四边形
两点.当这两条直线互相垂直,且四边形![]() 的周长为
的周长为![]() 时,点
时,点![]() 的坐标为_________.
的坐标为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com