
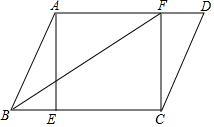
 如图,在平行四边形ABCD中,过点A作AE⊥BC交BC边于点E,点F在边AD上,且DF=BE.
如图,在平行四边形ABCD中,过点A作AE⊥BC交BC边于点E,点F在边AD上,且DF=BE.分析 (1)首先证明AF=EC,AF∥EC,推出四边形AECF是平行四边形,再证明∠AEC=90°即可解决问题;
(2)分别在Rt△ABE,Rt△BCF中,利用勾股定理求出AE、BF即可;
解答 (1)证明: ∵四边形ABCD是平行四边形,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵BE=DF,
∴AF=EC,
∴四边形AECF是平行四边形,
∵AE⊥BC,
∴∠AEC=90°,
∴四边形AECF是矩形.
(2)解:∵BF平分∠ABC,AD∥BC,
∴∠ABF=∠CBF=∠AFB,
∴AB=AF=3,AD=BC=4,
在Rt△ABE中,AE=CF=$\sqrt{A{B}^{2}-B{E}^{2}}$=2$\sqrt{2}$,
在Rt△BFC中,BF=$\sqrt{B{C}^{2}+C{F}^{2}}$=$\sqrt{{4}^{2}+(2\sqrt{2})^{2}}$=2$\sqrt{6}$.
点评 本题考查平行四边形的性质、矩形的判定和性质、勾股定理、等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:填空题
 在数学课上,老师提出如下问题:已知:直线AB和直线AB外一点O.
在数学课上,老师提出如下问题:已知:直线AB和直线AB外一点O.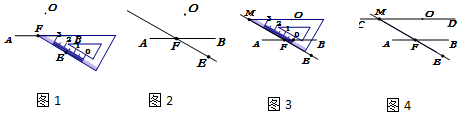
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | ①②③④ | B. | ④①③② | C. | ④②③① | D. | ④③②① |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
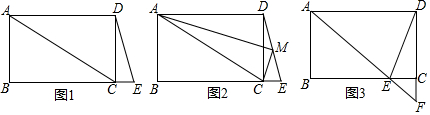
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
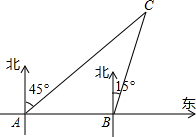 钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com