
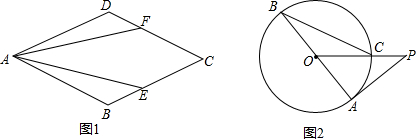
分析 (1)根据菱形的性质,利用SAS判定△ABE≌△ADF,从而求得AE=AF;
(2)利用切线的性质和直角三角形的两个锐角互余的性质得到圆心角∠PAO的度数,然后利用圆周角定理来求∠ABC的度数.
解答 证明:(1)∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠B=∠D
∵CE=CF,
∴BE=DF
在△ABE与△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠B=∠D}\\{BE=DF}\end{array}\right.$,
∴△ABE≌△ADF.
∴AE=AF;
(2)∵AB是⊙O的直径,直线PA与⊙O相切于点A,
∴∠PAO=90°.
又∵∠OPA=40°,
∴∠POA=50°,
∴∠ABC=$\frac{1}{2}$∠POA=25°.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.同时考查了切线的性质,圆周角定理.圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:解答题
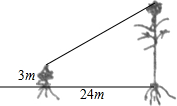 有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m远的一棵大树上,大树高14m,且巢离树顶部1m,当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,那它至少需要多少时间才能赶回巢中?(画出符合题意的几何图形,并求解)
有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m远的一棵大树上,大树高14m,且巢离树顶部1m,当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,那它至少需要多少时间才能赶回巢中?(画出符合题意的几何图形,并求解)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 2x | 3 | 2 |
| y | -3 | |
| 4y |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$-$\sqrt{2}$=3 | B. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | C. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | D. | $\sqrt{(-15)^{2}}$=-15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com