
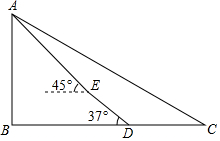
 今年国庆节,小明与爸爸一起去省级风景名胜区彭祖山游览,小明想估算彭祖山AB的高度,如图,他在距山脚下400米的C点测得山顶的仰角为30°,来到山脚下D点,沿37°斜坡DE走400米到彭祖墓前,测得山顶的仰角为45°,请你帮助小明估算一下彭祖山的高度.(结果精确到1m)(参考数据:$\sqrt{3}$=1.732,$\sqrt{2}$=1.414,sin37°=0.6,cos37°=0.8,tan37°=0.75,cot37°=1.33)
今年国庆节,小明与爸爸一起去省级风景名胜区彭祖山游览,小明想估算彭祖山AB的高度,如图,他在距山脚下400米的C点测得山顶的仰角为30°,来到山脚下D点,沿37°斜坡DE走400米到彭祖墓前,测得山顶的仰角为45°,请你帮助小明估算一下彭祖山的高度.(结果精确到1m)(参考数据:$\sqrt{3}$=1.732,$\sqrt{2}$=1.414,sin37°=0.6,cos37°=0.8,tan37°=0.75,cot37°=1.33) 分析 作EF⊥BC、EG⊥AB,在Rt△DEF中,可得BG=EF=DEsin∠EDF=240、DF=DEcos∠EDF=320,设AG=x,在Rt△AGE中,由∠AEG=45°可得BF=EG=AG=x,最后在Rt△ABC中由tanC=$\frac{AB}{BC}$可得关于x的方程,解之求得x即可知答案.
解答 解:作EF⊥BC于点F,作EG⊥AB于点G,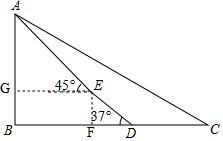
在Rt△DEF中,∵DE=400,∠EDF=37°,
∴BG=EF=DEsin∠EDF=400×0.6=240(m),
DF=DEcos∠EDF=400×0.8=320(m),
设AG=x,
在Rt△AGE中,∵∠AEG=45°,
∴BF=EG=AG=x,
在Rt△ABC中,∵∠C=30°,CD=400m,
∴tanC=$\frac{AB}{BC}$,即$\frac{x+240}{x+320+400}$=$\frac{\sqrt{3}}{3}$,
解得:x=240$\sqrt{3}$≈416,
则山高AB=AG+BG=416+240=656(m),
答:彭祖山的高度约为656米.
点评 本题主要考查解直角三角形的应用-仰角俯角问题,掌握仰角俯角的定义是解题的根本,根据题意构建合适的直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,∠BAC=45°,AE是∠BAC的平分线,CD⊥AB于D,交AE于点F.请探索AF与BC之间的数量关系,并说明理由.
如图,在△ABC中,AB=AC,∠BAC=45°,AE是∠BAC的平分线,CD⊥AB于D,交AE于点F.请探索AF与BC之间的数量关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
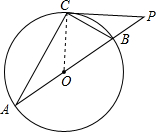 如图,AB是圆O直径,C是圆O上一点,P在AB延长线上,且∠PCB=∠A.
如图,AB是圆O直径,C是圆O上一点,P在AB延长线上,且∠PCB=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知∠B=∠DEC,AB=DE,要推得△ABC≌△DEC;
如图,已知∠B=∠DEC,AB=DE,要推得△ABC≌△DEC;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com