
【题目】大丰区在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗5棵,B种树苗10棵,需要1300元;购买A种树苗3棵,B种树苗5棵,需要710元.
(1)求购买A,B两种树苗每棵各需要多少元?
(2)现需购进这两种树苗共100棵,其中A种树苗购进x棵,考虑到绿化效果和资金周转,A种树苗不能少于30棵,且用于购买这两种树苗的资金不能超过8650元,试求x 的取值范围。
(3)某包工队承包了该项种植任务,若种好一棵A种树苗需付工钱15元,种好一棵B种树苗需付工钱25元,在(2)的条件下,设种好这100棵树苗共需付工钱y元,,试求出y与x的函数表达式,并写出所付的种植工钱最少的购买方案及最少工钱是多少元。
【答案】(1)A种树苗每棵需要120元,B种树苗每棵需要70元;(2)![]() ,x为整数;(3)y=-10x+2500,购买A种树苗33棵、B种树苗67棵时所付的种植工钱最少,最少工钱是2170元.
,x为整数;(3)y=-10x+2500,购买A种树苗33棵、B种树苗67棵时所付的种植工钱最少,最少工钱是2170元.
【解析】
(1)设购买A种树苗每棵需要x元,B种树苗每棵需要y元,根据总价=单价×数量,可列出关于x、y的二元一次方程组,解方程组即可得出结论;
(2)设购买A种树苗m棵,则购买B种树苗(100-m)棵,根据总价=单价×数量,可列出关于m的一元一次不等式组,解不等式组即可得出m的取值范围,由此可得出结论;
(3)设种植工钱为W,根据植树的工钱=植A种树的工钱+植乙种数的工钱,列出W关于m的函数关系式,根据一次函数的单调性即可解决最值问题.
(1)设购买A种树苗每棵需要x元,B种树苗每棵需要y元,
由题意得:
![]() ,
,
解得:![]() .
.
答:购买A种树苗每棵需要120元,B种树苗每棵需要70元.
(2)设购买A种树苗m棵,则购买B种树苗(100-m)棵,
根据已知,得
![]() ,
,
解得:30≤m≤33.
故有四种购买方案:
方案1、购买A种树苗30棵,B种树苗70棵;
方案2、购买A种树苗31棵,B种树苗69棵;
方案3、购买A种树苗32棵,B种树苗68棵;
方案4、购买A种树苗33棵,B种树苗67棵.
(3)设种植工钱为W,由已知得:
W=15m+25(100-m)=-10m+2500,
∵-10<0,y随x的增大而减小,
∴当m=33时,y最小,最小值为2170元..
故购买A种树苗33棵、B种树苗67棵时所付的种植工钱最少,最少工钱是2170元.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在平面直角坐标系中,点O坐标原点,直线l分别交x轴、y轴于A,B两点,OA<OB,且OA、OB的长分别是一元二次方程![]() 的两根.
的两根.
(1)求直线AB的函数表达式;
(2)点P是y轴上的点,点Q第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为4,把三角板的直角顶点放置BC中点E处,三角板绕点E旋转,三角板的两边分别交边AB、CD于点G、F.
(1)求证:△GBE∽△GEF.
(2)设AG=x,GF=y,求Y关于X的函数表达式,并写出自变量取值范围.
(3)如图2,连接AC交GF于点Q,交EF于点P.当△AGQ与△CEP相似,求线段AG的长.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A,B在x轴上,且关于y轴对称,反比例函数y=![]() (x>0)的图象经过点C,反比例函数y=
(x>0)的图象经过点C,反比例函数y=![]() (x<0)的图象分别与AD,CD交于点E,F,若S△BEF=7,k1+3k2=0,则k1等于_____.
(x<0)的图象分别与AD,CD交于点E,F,若S△BEF=7,k1+3k2=0,则k1等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
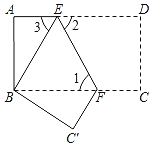
(1)折叠后,DC的对应线段是 ,CF的对应线段是 .
(2)若∠1=55°,求∠2、∠3的度数;
(3)若AB=6,AD=12,求△BC′F的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
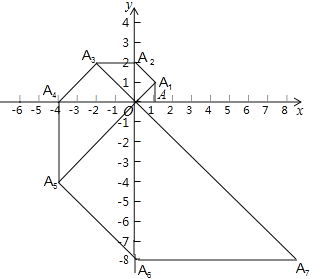
【题目】如图,在平面直角坐标系中,等腰直角三角形OAA1的直角边OA在x轴上,点A1在第一象限,且OA=1,以点A1为直角顶点,0A1为一直角边作等腰直角三角形OA1A2,再以点A2为直角顶点,OA2为直角边作等腰直角三角形OA2A3…依此规律,则点A2019的坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com