
【题目】已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,
(1)证明ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)先证得△ADB≌△CDB求得∠BCD=∠BAD,从而得到∠ADF=∠BAD,所以AB∥FD,因为BD⊥AC,AF⊥AC,所以AF∥BD,即可证得.
(2)先证得平行四边形是菱形,然后根据勾股定理即可求得.
试题解析:(1)证明:∵BD垂直平分AC,
∴AB=BC,AD=DC,
在△ADB与△CDB中,
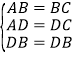 ,
,
∴△ADB≌△CDB(SSS)
∴∠BCD=∠BAD,
∵∠BCD=∠ADF,
∴∠BAD=∠ADF,
∴AB∥FD,
∵BD⊥AC,AF⊥AC,
∴AF∥BD,
∴四边形ABDF是平行四边形,
(2)解:∵四边形ABDF是平行四边形,AF=DF=5,
∴ABDF是菱形,
∴AB=BD=5,
∵AD=6,
设BE=x,则DE=5-x,
∴AB2-BE2=AD2-DE2,
即52-x2=62-(5-x)2
解得:x=![]() ,
,
∴![]() ,
,
∴AC=2AE=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
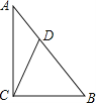
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,cosA=![]() ,点D是斜边AB上的动点且不与A,B重合,连接CD,点B'与点B关于直线CD对称,连接B'D,当B'D垂直于Rt△ABC的直角边时,BD的长为______.
,点D是斜边AB上的动点且不与A,B重合,连接CD,点B'与点B关于直线CD对称,连接B'D,当B'D垂直于Rt△ABC的直角边时,BD的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第1个正方形的面积为___;第4个正方形的面积为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
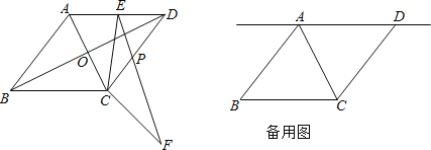
【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,已知AC=2![]() ,AB=5.
,AB=5.
(1)求BD的长;
(2)点E为直线AD上的一个动点,连接CE,将线段EC绕点C顺时针旋转∠BCD的角度后得到对应的线段CF(即∠ECF=∠BCD),EF交CD于点P.
①当E为AD的中点时,求EF的长;
②连接AF、DF,当DF的长度最小时,求△ACF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).

(1)试作出△ABC以C为旋转中心,沿顺时针方向旋转90°后的图形△A1B1C;
(2)以原点O为对称中心,再画出与△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
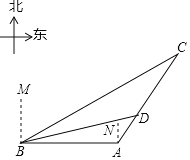
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为![]() 元/件(
元/件(![]() ,且
,且![]() 是按0.5元的倍数上涨),当天销售利润为
是按0.5元的倍数上涨),当天销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过![]() ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
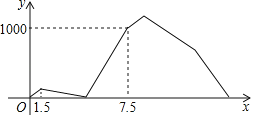
【题目】甲乙两人从A地出发去相距1800米的B地,甲出发1.5分钟后乙再出发,在中途乙追上甲,追上甲后,乙发现有东西忘带了,于是以原来1.2倍的速度返回,甲则继续以原速度前行,乙返回A地后取东西花了2分钟,取完东西后立即以返回时的速度追甲,甲达到B地以后立即返回,并与乙在途中相遇,设甲乙两人之间的距离为y(米),甲出发的时间为x(分钟),y与x的关系如图所示,则当甲乙两人第二次相遇时,两人距B地的距离为_____米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com