
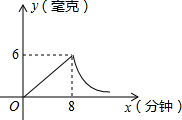
 为了预防流行性感冒,某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时室内每立方米空气中的含药量y毫克)与时间x(分钟)成正比例;药物燃烧后,y与x成反比例(如图所示).请根据图中提供的信息,解答下列问题:
为了预防流行性感冒,某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时室内每立方米空气中的含药量y毫克)与时间x(分钟)成正比例;药物燃烧后,y与x成反比例(如图所示).请根据图中提供的信息,解答下列问题:分析 (1)由于在药物燃烧阶段后,y与x成反比例,因此设函数解析式为y=$\frac{k}{x}$(k≠0),然后由(8,6)在函数图象上,利用待定系数法即可求得药物燃烧阶段后y与x的函数解析式;
(2)把y=1.6代入反比例函数解析式,求出相应的x;
(3)把y=3代入正比例函数解析式和反比例函数解析式,求出相应的x,两数之差与10进行比较,>等于10就有效.
解答 解:(1)∵药物燃烧完毕后,y与x成反比例
∴设 y=$\frac{{k}_{1}}{x}$,
∵(8,6)在y=$\frac{{k}_{1}}{x}$上,
∴k1=6×8=48;
∴y=$\frac{48}{x}$;
故答案为:y=$\frac{48}{x}$;
(2)把y=1.6代入y=$\frac{48}{x}$,
得x=30
故学生至少经过30分钟才可以进课室;
(3)设药物燃烧时y关于x的函数关系式为y=k2x(k2>0)代入(8,6)为6=8k2
∴k2=$\frac{3}{4}$,
∴药物燃烧时y关于x的函数关系式为y=$\frac{3}{4}$x(0≤x≤8)
把y=3代入y=$\frac{3}{4}$x,得:x=4
把y=3代入y=$\frac{48}{x}$,得:x=16
∵16-4=12
所以这次消毒是有效的.
点评 本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
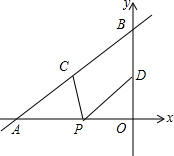 如图,直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )
如图,直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为( )| A. | (-3,0) | B. | (-6,0) | C. | (-$\frac{3}{2}$,0) | D. | (-$\frac{5}{2}$,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
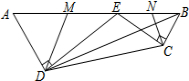 如图,在四边形ABCD中,E为AB边上一点,ED⊥AD于D,EC⊥CB于C,且∠AED=∠BEC,AB=2$\sqrt{13}$,AD=3,BD=$\sqrt{37}$,M、N分别为AE、BE的中点,连接DM、CN,则△DEM与△CEN的周长之和为2$\sqrt{13}$+6.
如图,在四边形ABCD中,E为AB边上一点,ED⊥AD于D,EC⊥CB于C,且∠AED=∠BEC,AB=2$\sqrt{13}$,AD=3,BD=$\sqrt{37}$,M、N分别为AE、BE的中点,连接DM、CN,则△DEM与△CEN的周长之和为2$\sqrt{13}$+6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月用水量 | 不超过12m3的部分 | 超过12m3的部分不超过18m3的部分 | 超过18m3的部分 |
| 收费标准(元/m3) | 2 | 2.5 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
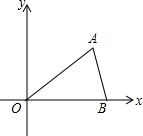 如图,在平面直角坐标系中,点A($\sqrt{3}$,1)、B(2,0)、O(0,0),反比例函数y=$\frac{k}{x}$图象过点A.
如图,在平面直角坐标系中,点A($\sqrt{3}$,1)、B(2,0)、O(0,0),反比例函数y=$\frac{k}{x}$图象过点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com